Performance of the VLA during the Next Semester
Introduction
This section contains details of the VLA's resolution, expected sensitivity, tuning range, dynamic range, pointing accuracy, and modes of operation. Detailed discussions of most of the observing limitations are found elsewhere. In particular, see References 1 and 2, listed in the Documentation.
Resolution
The VLA's resolution is generally diffraction-limited, and thus is set by the array configuration and frequency of observation. It is important to be aware that a synthesis array is "blind" to structures on angular scales both smaller and larger than the range of fringe spacings given by the antenna distribution. For the former limitation, the VLA acts like any single antenna - structures smaller than the diffraction limit (θ ∼ λ/D) are not seen -- the resulting image will be smoothed to the resolution of the array. The latter limitation is unique to interferometers; it means that structures on angular scales significantly larger than the fringe spacing formed by the shortest baseline are not measured. No subsequent processing can fully recover this missing information, which can only be obtained by observing in a smaller array configuration, by using the mosaicing method, or by utilizing data from an instrument (such as a large single antenna or an array comprising smaller antennas) which provides this information.
Table 5 summarizes the relevant information. This table shows the maximum and minimum antenna separations, the approximate synthesized beam size (full width at half-power) for the central frequency for each band, and the scale at which severe attenuation of large scale structure occurs.
| Configuration | A | B | C | D |
|---|---|---|---|---|
| Bmax (km1) | 36.4 | 11.1 | 3.4 | 1.03 |
| Bmin (km1) | 0.68 | 0.21 | 0.0355 | 0.035 |
| Band |
Synthesized Beamwidth θHPBW(arcsec)1,2,3 | |||
| 74 MHz (4) | 24 | 80 | 260 | 850 |
| 350 MHz (P) | 5.6 | 18.5 | 60 | 200 |
| 1.5 GHz (L) | 1.3 | 4.3 | 14 | 46 |
| 3.0 GHz (S) | 0.65 | 2.1 | 7.0 | 23 |
| 6.0 GHz (C) | 0.33 | 1.0 | 3.5 | 12 |
| 10 GHz (X) | 0.20 | 0.60 | 2.1 | 7.2 |
| 15 GHz (Ku) | 0.13 | 0.42 | 1.4 | 4.6 |
| 22 GHz (K) | 0.089 | 0.28 | 0.95 | 3.1 |
| 33 GHz (Ka) | 0.059 | 0.19 | 0.63 | 2.1 |
| 45 GHz (Q) | 0.043 | 0.14 | 0.47 | 1.5 |
| Largest Angular Scale θLAS(arcsec)1,4 | ||||
| 74 MHz (4) | 800 | 2200 | 20000 | 20000 |
| 350 MHz (P) | 155 | 515 | 4150 | 4150 |
| 1.5 GHz (L) | 36 | 120 | 970 | 970 |
| 3.0 GHz (S) | 18 | 58 | 490 | 490 |
| 6.0 GHz (C) | 8.9 | 29 | 240 | 240 |
| 10 GHz (X) | 5.3 | 17 | 145 | 145 |
| 15 GHz (Ku) | 3.6 | 12 | 97 | 97 |
| 22 GHz (K) | 2.4 | 7.9 | 66 | 66 |
| 33 GHz (Ka) | 1.6 | 5.3 | 44 | 44 |
| 45 GHz (Q) | 1.2 | 3.9 | 32 | 32 |
- These estimates of the synthesized beamwidth are for a uniformly weighted, untapered map produced from a full 12 hour synthesis observation of a source which passes near the zenith.
- Footnotes:
- 1. Bmax is the maximum antenna separation, Bmin is the minimum antenna separation, θHPBW is the synthesized beam width (FWHM), and θLAS is the largest scale structure "visible" to the array.
- 2. The listed resolutions are appropriate for sources with declinations between −15 and 75 degrees. For sources outside this range, the extended north arm hybrid configurations (DnC, CnB, BnA) should be used, and will provide resolutions similar to the smaller configuration of the hybrid, except for declinations south of −30. No double-extended north arm hybrid configuration (e.g., DnB, or CnA) is provided.
- 3. The approximate resolution for a naturally weighted map is about 1.5 times the numbers listed for θHPBW. The values for snapshots are about 1.3 times the listed values.
- 4. The largest angular scale structure is that which can be imaged reasonably well in full synthesis observations. For single snapshot observations the quoted numbers should be divided by two.
- 5. For the C configuration an antenna from the middle of the north arm is moved to the central pad "N1". This results in improved imaging for extended objects, but may slightly degrade snapshot performance. Note that although the minimum spacing is the same as in D configuration, the surface brightness sensitivity and image fidelity to extended structure is considerably inferior to that of the D configuration.
A project with the goal of doubling the longest baseline available in the A configuration by establishing a real-time fiber optic link between the VLA and the VLBA antenna at Pie Town was established in the late 1990s, and used through 2005. This link is no longer operational; the goal of implementing a new digital Pie Town link, now that EVLA construction is complete, remains unfunded.
Sensitivity
The theoretical thermal noise expected for an image using natural weighting of the visibility data is given by:
| \[\Delta I_m = \frac{SEFD}{\eta_{\rm c}\sqrt{n_{\rm pol}N(N-1)t_{\rm int}\Delta\nu}}\] | (eq. 1) |
where:
- - SEFD is the "system equivalent flux density" (Jy), defined as the flux density of a radio source that doubles the system temperature. Lower values of the SEFD indicate more sensitive performance. For the VLA's 25-meter paraboloids, the SEFD is given by the equation SEFD = 5.62Tsys/ηA, where Tsys is the total system temperature (receiver plus antenna plus sky), and ηA is the antenna aperture efficiency in the given band.
- - ηc is the correlator efficiency (at least 0.92 for the VLA).
- - npol is the number of polarization products included in the image; npol = 2 for images in Stokes I, Q, U, or V, and npol = 1 for images in 'RCP' or 'LCP'.
- - N is the number of antennas.
- - tint is the total on-source integration time in seconds.
- - Δν is the bandwidth in Hz.
Figure 1 shows the SEFD as a function of frequency for those bands currently installed on VLA antennas, and include the contribution to Tsys from atmospheric emission at the zenith. Table 6 gives the SEFD at some fiducial VLA frequencies.
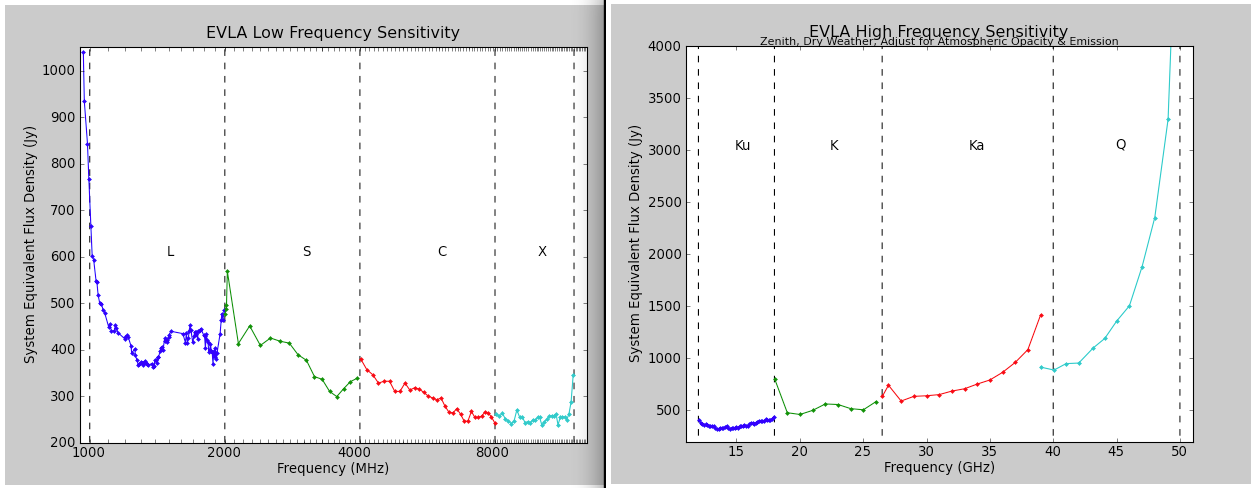
| Frequency | SEFD | RMS confusion level |
|---|---|---|
| (Jy) | in D config (µJy/beam) | |
| 0.37 GHz (P) | 3900 | 4200 |
| 1.5 GHz (L) | 420 | 89 |
| 3.0 GHz (S) | 370 | 14 |
| 6.0 GHz (C) | 310 | 2.3 |
| 10.0 GHz (X) | 250 | negligible |
| 15 GHz (Ku) | 350 | negligible |
| 22 GHz (K) | 560 | negligible |
| 33 GHz (Ka) | 730 | negligible |
| 45 GHz (Q) | 1400 | negligible |
- Note: SEFDs at Ku, K, Ka, and Q bands include contributions from Earth's atmosphere, and were determined under good conditions.
Note that the theoretical rms noise calculated using equation 1 is the best limit possible. There are several factors that will tend to increase the noise compared with theoretical:
- For the more commonly-used "robust" weighting scheme, intermediate between pure natural and pure uniform weightings (available in the AIPS task IMAGR and CASA task clean), typical parameters will result in the sensitivity being a factor of about 1.2 worse than the listed values.
- Confusion. There are two types of confusion: (i) that due to confusing sources within the synthesized beam, which affects low resolution observations the most. Table 6 shows the confusion noise in D configuration (see Condon 2002, ASP Conf. 278, 155), which should be added in quadrature to the thermal noise in estimating expected sensitivities. The confusion limits in C configuration are approximately a factor of 10 less than those in Table 6; (ii) confusion from the sidelobes of uncleaned sources lying outside the image, often from sources in the sidelobes of the primary beam. This primarily affects low frequency observations.
- Weather. The sky and ground temperature contributions to the total system temperature increase with decreasing elevation. This effect is very strong at high frequencies, but is relatively unimportant at the other bands. The extra noise comes directly from atmospheric emission, primarily from water vapor at K-band, and from water vapor and the broad wings of the strong 60 GHz O2 transitions at Q-band.
- Losses from the 3-bit samplers. The VLA's 3-bit samplers incur an additional 10 to 15% loss in sensitivity above that expected -- i.e., the efficiency factor ηc = 0.78 to 0.83.
- In general, the zenith atmospheric opacity to microwave radiation is very low - typically less than 0.01 at L, C and X-bands, 0.05 to 0.2 at K-band, and 0.05 to 0.1 at the lower half of Q-band, rising to 0.3 by 49 GHz. The opacity at K-band displays strong variations with time of day and season, primarily due to the 22 GHz water vapor line. Conditions are best at night, and in the winter. Q-band opacity, dominated by atmospheric O2, is considerably less variable.
- Observers should remember that clouds, especially clouds with large water droplets (read, thunderstorms!), can add appreciable noise to the system temperature. Significant increases in system temperature can, in the worst conditions, be seen at frequencies as low as 5 GHz.
- Tipping scans can be used for deriving the zenith opacity during an observation. In general, tipping scans should only be needed if the calibrator used to set the flux density scale is observed at a significantly different elevation than the range of elevations over which the phase calibrator and target source are observed. However, the antenna tip capability is currently unavailable for the upgraded VLA -- it is hoped that this will again be available in the next year.
- When the flux density calibrator observations are within the elevation range spanned by the science observing, elevation dependent effects (including both atmospheric opacity and antenna gain dependencies) can be accounted for by fitting an elevation-dependent gain term. See the following item.
- Antenna elevation-dependent gains. The antenna figure degrades at low elevations, leading to diminished forward gain at the shorter wavelengths. The gain-elevation effect is negligible at frequencies below 8 GHz. The antenna gains can be determined by direct measurement of the relative system gain using the AIPS task ELINT on data from a strong calibrator which has been observed over a wide range of elevation. If this is not possible, care should be taken to observe a primary flux calibrator at the same elevation as the target.
Both CASA and AIPS allow the application of elevation-dependent gains and an estimated opacity generated from ground-based weather (e.g., through the tasks gencal and plotweather in CASA, and INDXR in AIPS).
- Pointing. The SEFD quoted above assumes good pointing. Under calm nighttime conditions, the antenna blind pointing is about 10 arcsec rms. The pointing accuracy in daytime can be much worse -- occasionally exceeding 1 arcminte, due to the effects of solar heating of the antenna structures. Moderate winds have a very strong effect on both pointing and antenna figure. The maximum wind speed recommended for high frequency observing is 15 mph (7 m/s). Wind speeds near the stow limit (45 mph) will have a similar negative effect at 8 and 15 GHz.
- To achieve better pointing, "referenced pointing" is recommended, where a nearby calibrator is observed in interferometer pointing mode every hour or so. The local pointing corrections thus measured can then be applied to subsequent target observations. This reduces rms pointing errors to as little as 2 - 3 arcseconds (but more typically 5 to 7 arcseconds) if the reference source is within about 15 degrees (in azimuth and elevation) of the target source, and the source elevation is less than 70 degrees. At source elevations greater than 80 degrees (zenith angle < 10 degrees), source tracking becomes difficult; it is recommended to avoid such source elevations during the observation preparation setup.
- Use of referenced pointing is highly recommended for all Ku, K, Ka, and Q-band observations, and for lower frequency observations of objects whose total extent is a significant fraction of the antenna primary beam. It is usually recommended that the referenced pointing measurement be made at 8 GHz (X-band), regardless of what band your target observing is at, since X-band is the most sensitive, and the closest calibrator is likely to be weak. Proximity of the reference calibrator to the target source is of paramount importance; ideally the pointing sources should precede the target by 20 or 30 minutes in Right Ascension (RA). The calibrator should have at least 0.3 Jy flux density at X-band and be unresolved on all baselines to ensure an accurate solution.
To aid VLA proposers there is an on-line Exposure Calculator tool that provides a graphical user interface to these equations.
Special caveats apply for P-band (235 -- 490 MHz) observing. The listed SEFD in table 6 is from an observation taken far from the Galactic plane, where the sky brightness is about 30K. At this band, Galactic synchrotron emission is very bright in directions near the Galactic plane. The system temperature increase due to Galactic emission will degrade sensitivity by factors of two to three for observations in the plane, and by a factor of 5 or more at or near the Galactic center. In addition, the antenna efficiency (currently about 0.31 for 300 MHz) will decline with both increasing and decreasing frequencies from the center of P-band.
The beam-averaged brightness temperature measured by a given array depends on the synthesized beam, and is related to the flux density per beam by:
| \[T_{\rm b} = \frac{S \lambda^2}{2k\Omega} = F \cdot S\] | (eq. 2) |
-
-
- where Tb is the brightness temperature (Kelvins) and Ω is the beam solid angle. For natural weighting (where the angular size of the approximately Gaussian beam is ∼ 1.5λ/Bmax), and S in mJy per beam, the constant F depends only upon array configuration and has the approximate value F = 190, 18, 1.7, 0.16 for A, B, C, and D configurations, respectively. The brightness temperature sensitivity can be obtained by substituting the rms noise, ΔIm, for S. Note that Equation 2 is a beam-averaged surface brightness; if a source size can be measured the source size and integrated flux density should be used in Equation 2, and the appropriate value of F calculated. In general the surface brightness sensitivity is also a function of the source structure and how much emission may be filtered out due to the sampling of the interferometer. A more detailed description of the relation between flux density and surface brightness is given in Chapter 7 of Reference 1, listed in Documentation.
-
For observers interested in HI in galaxies, a number of interest is the sensitivity of the observation to the HI mass. This is given by van Gorkom et al. (1986; AJ, 91, 791):
| \[M_{\rm HI} = 2.36 \times 10^5 D^2 \sum S \Delta V ~M_\odot\] | (eq. 3) |
where D is the distance to the galaxy in Mpc, and SΔV is the HI line area in units of Jy km/s.
VLA Frequency Bands and Tunability
Bands
For observations taken with the 8-bit samplers, each receiver can tune to two different frequencies, each 1.024 GHz wide, within the same frequency band. Right-hand circular (RCP) and left-hand circular (LCP) polarizations are received for both frequencies, except for the low-band receiver (50 -- 500 MHz), which provides linear polarization. Each of these four data streams follows the VLA nomenclature, and are known as IF (for "Intermediate Frequency" channel) "A", "B", "C", and "D". IFs A and B provide RCP, IFs C and D provide LCP. IFs A and C are always at the same frequency, as are IFs B and D (but note that the A and C IFs frequency is usually different from the B and D frequency). We normally refer to these two independent data streams as "IF pairs" -- i.e., the 'A/C' pair and the 'B/D' pair. In 8-bit mode, a maximum of 1.024 GHz can be correlated for each IF pair (see the WIDAR Section), for a total maximum bandwidth of 2.048 GHz. To distinguish this 8-bit system from the 3-bit system (described below), these IF pairs are denoted A0/C0 and B0/D0.
The tuning ranges, along with default frequencies for continuum applications, are given in Table 7 below.
| Band | Range1 | Default frequencies for continuum applications (GHz) | |
|---|---|---|---|
| (GHz) | IF pair A0/C0 | IF pair B0/D0 | |
| 4 m (4) | 0.058-0.084 | N.A. | .054 -- .086 |
| 90 cm (P) | 0.23-0.472 | 0.236 -- 0.492 | N.A. |
| 20 cm (L) | 1.0-2.03 | 1.0 -- 1.52 | 1.5 -- 2.02 |
| 13 cm (S) | 2.0-4.0 | 2.0 -- 3.0 |
3.0 -- 4.0 |
| 6 cm (C) | 4.0-8.0 | 4.5 -- 5.5 | 5.5 -- 6.5 |
| 3 cm (X) | 8.0-12.0 | 8.0 -- 9.0 | 9.0 -- 10.0 |
| 2 cm (Ku) | 12.0-18.0 | 13.0 -- 14.0 |
14.0 -- 15.0 |
| 1.3 cm (K) | 18.0-26.5 | 20.2 -- 21.2 |
21.2 -- 22.2 |
| 1 cm (Ka) | 26.5-40.0 | 32.0 -- 33.0 |
31.0 -- 32.0 |
| 0.7 cm (Q) | 40.0-50.0 | 40.0 -- 41.0 |
41.0 -- 42.0 |
- Notes:
- 1. Listed here are the nominal band edges. For all bands, the receivers can be tuned to frequencies outside this range, but at the cost of diminished performance. Contact VLA staff for further information.
- 2. The default setup for P-band will provide two subbands from the A0D0 IF pair, each 128 MHz wide, spanning 236 -- 364 MHz, and 364 -- 492 MHz. The channel resolution is 125 kHz. The B0D0 pair will be used for the 4-band tuning.
- 3. The default frequency set-up for L-band comprises two 512 MHz IF pairs (each comprising 8 contiguous subbands of 64 MHz) to cover the entire 1-2 GHz of the L-band receiver.
Tuning Restrictions
In general, for all frequency bands except Ka, if the total span of the two independent IFs (defined as the frequency difference between the lower edge of one IF pair and the upper edge of the other) is less than 8.0 GHz, there are no restrictions on the frequency placements of the two IF pairs. For K, Ka and Q bands (the only bands where a span greater than 8 GHz is possible), there are special rules:
- At Ka band, the low frequency edge of the AC IF must be greater than 32.0 GHz. There is no restriction on the BD frequency, unless the BD band overlaps the AC band when the latter is tuned at or near the 32.0 GHz limit. In this case, the Observation Preparation Tool (OPT) may not allow the requested frequency setups. Users wanting to use such a frequency setup are encouraged to contact the NRAO Helpdesk for possible tuning options.
- At K and Q bands, if the frequency span is greater than 8.0 GHz, the BD frequency must be lower than the AC frequency.
With the 3-bit samplers, more options are available. This system provides four (R,L) polarization pairs, each 2048 MHz wide. The A/C IF pair provides two sampled pairs, labelled A1C1 and A2C2, and the B/D IF pair provides two sampled pairs, labelled B1D1 and B2D2. The maximum frequency span permitted for the A1C1 and A2C2 pairs is about 5000 MHz. The same restriction applies to B1D1 and B2D2. The tuning restrictions given above for the separation and location of the 8-bit pairs A0C0 and B0D0 also apply to the 3-bit pairs, with A0C0 replaced by A1C1 and A2C2, and B0D0 replaced by B1D1 and B2D2.
VLA Samplers
The 8-bit Set consists of four 8-bit samplers running at 2.048 GSamp/sec. The four samplers are arranged in two pairs, each pair providing 1024 MHz bandwidth in both polarizations. The two pairs are denoted A0/C0 and B0/D0. Taken together, the four samplers offer a maximum of 2048 MHz coverage with full polarization. The frequency spans sampled by the two pairs need not be adjacent. Some restrictions apply, depending on band, as described in the section on Frequency Bands and Tunability
The 3-bit Set consists of eight 3-bit samplers running at 4.096 GSamp/sec. The eight samplers are arranged as four pairs, each pair providing 2048 MHz bandwidth in both polarizations. Two of these pairs, denoted A1/C1 and A2/C2 cannot span more than 5000 MHz (lower edge of one to the higher edge of the other). The same limitation applies to the second pair, denoted B1/D1 and B2/D2. The tuning restrictions are described in the section on Frequency Bands and Tunability.
Which set to use?
- S, L, and 4/P-band observations, whether line or continuum, should use the 8-bit sampler set.
- C and X-band continuum observations should use 3-bit samplers in order to exploit the full 4 GHz bandwidth: in spite of the 15% reduction in sensitivity that comes with 3-bit (at equal bandwidth to the 8-bit samplers; see below for details) and the reduced effective bandwidth after removing RFI this still provides superior overall sensitivity. For more details we refer to EVLA memo 166.
- Ku, K, Ka, and Q band continuum observations should use the 3-bit samplers for maximum bandwidth.
- Wide-band spectral line searches requiring more than 2 GHz span should use the 3-bit samplers.
- Spectral-line observations which fit within two (possibly disjoint) 1 GHz bands should use the 8-bit set.
- Simultaneous continuum and high resolution spectral line observation can use mixed 3-bit and 8-bit samplers. The 3 bit samplers in this case will be set up to deliver the continuum data, while the 8-bit samplers will be for the spectral line data. The mix mode can be used in C and the higher frequency bands.
Major Characteristics of each Set
The 8-bit samplers are warranted for observations at 4/P-band, L-band, and S-band. The full analog bandwidth from the receivers fits within the 2048 MHz span covered by the samplers.
For the 3-bit samplers users need to be aware of the following issues:
- Sensitivity: compared to the 8-bit system, the sensitivity of the 3-bit samplers is worse by ~15% (at equal bandwidth). Alternatively, a given continuum noise level, requiring on-source integration time T with the 8-bit (two bands of 1GHz), requires 0.33T with the 3-bit (4 bands of 2GHz, assuming the bandwidth is available from the front end.)
- Resonances: each of the eight 3-bit samplers on an antenna has a resonance about 3 MHz wide. Each resonance is independent of all others, so there is no correlated signal between antennas. The resonance degrades the spectrum in its narrow frequency range, but has little effect on continuum observing. Bandpass solutions will be affected, but can be interpolated over. Spectral-line calibration and images at the affected frequencies will show significant loss in sensitivity. The resonances are easily seen in autocorrelation spectra, and it is recommended that users, especially spectral-line users, utilize these to locate the compromised frequencies.
- Amplitude Calibration: The traditional method for both 8- and 3-bit systems is to observe a flux-density calibrator, use self-cal to determine the antenna amplitude calibration factors (gains), and transfer the gains to the phase calibrator and target. For 3-bit samplers this procedure gives results good to 5%, between elevations of 20-70degrees. (Expect worse at the upper edge of Q-band and/or during bad weather). The SY (switched power) data can be used to correct for system gain variations and works well for the 8-bit samplers. For 3-bit samplers, the Pdif depends on the Psum, i.e. Pdif is non-linear, and its application will bias the resulting visibilities by 5 to 10%. The origin of this effect is understood, but we have not yet determined how best to compensate for it. Because of this, we do not recommend use of the 'Psum' and 'Pdif' data in the SY table, to calibrate visibilities from the 3-bit samplers. We do, however, recommend that the 'Requantizer Gains' in the SY table be applied to remove gain changes.. For more information about the switched power, and 'Psum' and 'Pdif, see EVLA memo 145.
Setting up the 8-bit or 3-bit Samplers
Either set requires an initial scan for each individual LO (frequency) tuning, during which power levels are optimized.
For the 8-bit system, a 'dummy scan' of 1 minute duration is sufficient for each tuning. This is usually done while the antennas are slewing at the start of an observing file, as the pointing direction of the antennas is not critical.
For the 3-bit system, the requirements are more demanding, see the example observing script. The minimum setup time is 1 minute for each tuning, to adjust the power levels and bandpass slopes across the 2GHz samplers. These values are retained and applied if the tuning is re-encountered in the same observation. In addition, every time the LO setup is changed, whether or not it is new (e.g. changing from 8-bit X-band reference pointing back to target), a scan of 30 seconds is needed to re-set the subband gains (requantizers) in the correlator. For better amplitude calibration at high frequencies, the 3-bit initial setup should be near the elevation of the target, so do it after the first 8-bit setup described above. For 3-bit observing without 8-bit (e.g. C or X-band, without reference pointing), the power variation with elevation is small so the 3-bit setup can be done at any elevation.
For settings that use a mix of 3-bit and 8-bit samplers, the guidelines to set up the 3-bit samplers should be followed.
Other issues
The overhead for setup of 3-bit samplers can eat into observing time, especially for projects with many different LO settings, and/or sources all over the sky, accompanied by a band change, reference pointing, and requantizer reset for each direction. The impact is most severe for short scheduling blocks.
Polarization testing conducted so far indicates no degradation of performance by using the 3-bit samplers.
Field of View
Primary Beam
The ultimate factor limiting the field of view is the diffraction-limited response of the individual antennas. An approximate formula for the full width at half power in arcminutes is: θPB = 45/νGHz. More precise measurements of the primary beam shape have been derived and are incorporated in AIPS (task PBCOR) and CASA (clean task and the imaging toolkit) to allow for correction of the primary beam attenuation in wide-field images. Objects larger than approximately half this angle cannot be directly observed by the array. However, a technique known as "mosaicing," in which many different pointings are taken, can be used to construct images of larger fields. Refer to References 1 and 2 in Documentation for details.
Guidelines for mosaicing with the VLA are given in the Guide to Observing with the VLA
Chromatic Aberration (Bandwidth Smearing)
The principles upon which synthesis imaging are based are strictly valid only for monochromatic radiation. When visibilities from a finite bandwidth are gridded as if monochromatic, aberrations in the image will result. These take the form of radial smearing which worsens with increased distance from the delay-tracking center. The peak response to a point source simultaneously declines in a way that keeps the integrated flux density constant. The net effect is a radial degradation in the resolution and sensitivity of the array.
These effects can be parameterized by the product of the fractional bandwidth (Δν/ν0) with the source offset in synthesized beamwidths (θ0/θHPBW). Table 8 shows the decrease in peak response and the increase in apparent radial width as a function of this parameter. Table 8 should be used to determine how much spectral averaging can be tolerated when imaging a particular field.
| (Δν/ν0)*(θ0/θHPBW) | Peak | Width |
|---|---|---|
| 0.0 | 1.00 | 1.00 |
| 0.50 | 0.95 | 1.05 |
| 0.75 | 0.90 | 1.11 |
| 1.0 | 0.80 | 1.25 |
| 2.0 | 0.50 | 2.00 |
- Note: The reduction in peak response and increase in width of an object due to bandwidth smearing (chromatic aberration). Δν/ν0 is the fractional bandwidth; θ0/θHPBW is the source offset from the phase tracking center in units of the synthesized beam.
Time-Averaging Loss
The sampled coherence function (visibility) for objects not located at the phase-tracking center is slowly time-variable due to the motion of the source through the interferometer coherence pattern, so that averaging the samples in time will cause a loss of amplitude. Unlike the bandwidth loss effect described above, the losses due to time averaging cannot be simply parametrized, except for observations at δ = 90°. In this case, the effects are identical to the bandwidth effect except they operate in the azimuthal, rather than the radial, direction. The functional dependence is the same as for chromatic aberration with Δν/ν0 replaced by ωeΔtint, where ωe is the Earth's angular rotation rate, and Δtint is the averaging interval.
For other declinations, the effects are more complicated and approximate methods of analysis must be employed. Chapter 13 of Reference 1 (in Documentation) considers the average reduction in image amplitude due to finite time averaging. The results are summarized in Table 9, showing the time averaging in seconds which results in 1%, 5% and 10% loss in the amplitude of a point source located at the first null of the primary beam. These results can be extended to objects at other distances from the phase tracking center by noting that the loss in amplitude scales with (θΔtint)2, where θ is the distance from the phase center and Δtint is the averaging time. We recommend that observers reduce the effect of time-average smearing by using integration times as short as 1 or 2 seconds (also see the section on Time Resolution and Data Rates) in the A and B configurations.
| Amplitude loss | |||
|---|---|---|---|
| Configuration | 1.0% | 5.0% | 10.0% |
| A | 2.1 | 4.8 | 6.7 |
| B | 6.8 | 15.0 | 21.0 |
| C | 21.0 | 48.0 | 67.0 |
| D | 68.0 | 150.0 | 210.0 |
- Note: The averaging time (in seconds) resulting in the listed amplitude losses for a point source at the antenna first null. Multiply the tabulated averaging times by 2.4 to get the amplitude loss at the half-power point of the primary beam. Divide the tabulated values by 4 if interested in the amplitude loss at the first null for the longest baselines.
Non-Coplanar Baselines
The procedures by which nearly all images are made in Fourier synthesis imaging are based on the assumption that all the coherence measurements are made in a plane. This is strictly true for E-W interferometers, but is false for the EVLA, with the single exception of snapshots. Analysis of the problem shows that the errors associated with the assumption of a planar array increase quadratically with angle from the phase-tracking center. Serious errors result if the product of the angular offset in radians times the angular offset in synthesized beams exceeds unity: θ > λB/D2, where B is the baseline length, D is the antenna diameter, and λ is the wavelength, all in the same units. This effect is most noticeable at λ90 and λ20 cm in the larger configurations, but will be notable in wide-field, high fidelity imaging for other bands and configurations.
Solutions to the problem of imaging wide-field data taken with non-coplanar arrays are well known, and have been implemented in AIPS (IMAGR) and CASA (clean). Refer to the package help files for these tasks, or consult with Rick Perley, Frazer Owen, or Sanjay Bhatnagar for advice. More computationally efficient imaging with non-coplanar baselines is being investigated, such as the "W-projection" method available in CASA; see EVLA Memo 67 (http://www.aoc.nrao.edu/evla/geninfo/memoseries/evlamemo67.pdf) for more details.
Time Resolution and Data Rates
The default integration times for the various array configurations are as follows:
| Configuration | Observing Bands | Default integration time |
|---|---|---|
| D, C |
L S C |
5 seconds |
| D, C |
X Ku K Ka Q |
3 seconds |
| B | all | 3 seconds |
| A | all | 2 seconds |
Observations with the 3-bit (wideband) samplers must use these integration times. Observations with the 8-bit samplers may use shorter integration times, but these must be requested and justified explicitly in the proposal, and obey the following restrictions:
| Minimum Integration Times and Maximum Data Rates (2014A) |
||
|---|---|---|
| Proposal type |
Minimum integration time |
Maximum data rate |
| Standard | 50 msec |
25 MB/s ( ~88 GB/hr) |
| Shared risk (SRO) | 50 msec | 60 MB/s (~210 GB/hr) |
Note that integration times as short as 5 msec and data rates as high as 300 MB/s can be supported for some observing, though any such observing is considered Resident Shared Risk Observing (RSRO). For these short integration times and high data rates there will be limits on bandwidth and/or number of antennas involved in the observation. Those desiring to utilize such short integration times and high data rates should consult with NRAO staff.
The maximum recommended integration time for any EVLA observing is 60 seconds. For high frequency observations with short scans (e.g., fast switching, as described in Rapid Phase Calibration and the Atmospheric Phase Interferometer (API)), shorter integration times may be preferable.
Observers should bear in mind the data rate of the VLA when planning their observations. For Nant antennas and integration time Δt, the data rate is:
| Data rate | = 45 MB/sec × (Nchpol/16384) x Nant × (Nant1)/(27×26) / (Δt/1 sec) |
| = 160 GB/hr × (Nchpol/16384) x Nant × (Nant1)/(27×26) / (Δt/1 sec) | |
| = 3.7 TB/day × (Nchpol/16384) x Nant × (Nant1)/(27×26) / (Δt/1 sec) | |
| ...equation (4) |
Here Nchpol is the sum over all subbands of spectral channels times polarization products:
| Nchpol = Σsb Nchan,i x Npolprod,i |
where Nchan,i is the number of spectral channels in subband i, and Npolprod,i is the number of polarization products for subband i (1 for single polarization [RR or LL], 2 for dual polarization [RR & LL], 4 for full polarization products [RR, RL, LR, LL]). This formula, combined with the maximum data rates given above, imply that observations using the maximum number of channels currently available (16384) will be limited to minimum integration times of ~2 seconds for standard observations, and 0.8 seconds for shared risk observations.
These data rates are challenging for data transfer, as well as data analysis. Currently data may either be downloaded via ftp within the Science Operations Centers, or mailed on hard drives for those not in the same building as the archive. The Archive Access Tool allows some level of frequency averaging to decrease data set sizes before ftp, for users whose science permits; note that the full spectral resolution will be retained in the NRAO archive for all observations.
Higher time resolutions and data rates are possible in principle but will be considered only through the Resident Shared Risk program.
Radio-Frequency Interference
The very wide bandwidths of the upgraded Very Large Array mean that RFI (radio-frequency interference) will be present in a far larger fraction of VLA observations than in observations made with the old systems. Considerable effort has gone into making the VLA's new electronics as linear as possible, so that the effects of any RFI will remain limited to the actual frequencies at which the RFI exists. Non-linear effects, such as receiver saturation, should occur only for those very unlikely, and usually very brief, times when the emitter is within the antenna primary beam.
RFI is primarily a problem within the low frequency bands (C, S, L, and the low-band system), and is most serious to the D configuration. With increasing frequency and increasing resolution comes an increasing fringe rate, which is often very effective in reducing interference to tolerable levels.
The bands within the tuning range of the VLA which are allocated exclusively to radio astronomy are 1400-1427 MHz, 1660-1670 MHz, 2690-2700 MHz, 4990-5000 MHz, 10.68-10.7 GHz, 15.35-15.4 GHz, 22.21-22.5 GHz, 23.6-24.0 GHz, 31.3-31.8 GHz, and 42.5-43.5 GHz. No external interference should occur within these bands.
RFI seen in VLA data can be internal or external. Great effort has been expended to eliminate all internally-generated RFI. Nevertheless, some internal RFI remains, which we are working hard to eliminate. Nearly all such internally-generated signals are at multiples of 128 MHz. So far as we know, all such internal signals are unresolved in frequency, and hence will affect only a single channel.
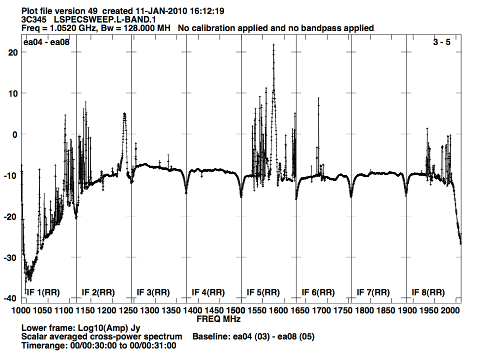
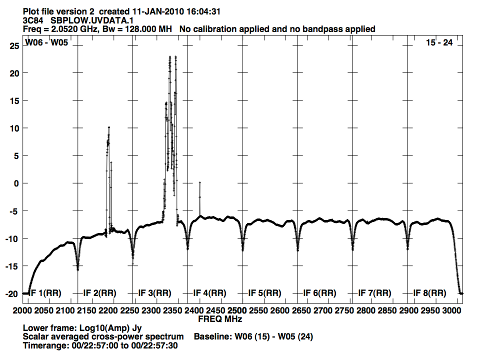
Radio frequency interference of external origin will be an increasing problem to astronomical observations. Table 10 lists some of the sources of external RFI at the VLA site that might be observed within the VLA's expanded tuning range within L and S bands. Figure 3 shows a raw power cross-power spectrum at L-band. Figure 4 shows a similar plot for the lower half of S-band.
|
Figure 3: Spectrum of L-band RFI. This shows the major interfering signals seen across the full 1 GHz bandwidth available to the L-band receivers. Each of the eight "spectral windows" displays 128 MHz from a separate sub-band. These are raw data, uncalibrated for the bandpass of either the digital filter or the receiver. The high linearity of the EVLA's electronics and correlator will permit astronomical observing within any frequencies not containing external interference. Note that the y-axis is in logarithmic units (dB). |
|---|---|
|
Figure 4: Spectrum of S-band RFI. This shows the raw spectrum of the lower half of S-Band - 2.0 to 3.0 GHz. The major interference at 2.35 GHz is from satellite radio. The y-axis is in logarithmic units (dB). |
| Frequency (MHz) | Source | Comments |
|---|---|---|
| 1025-1150 | Aircraft navigation | Very strong |
| 1200.0 | VLA modem | |
| 1217-1237 | GPS L2 | Very strong |
| 1243-1251 | GLONASS L2 | |
| 1254 | Aeronautical radar | |
| 1263 | Aeronautical radar | |
| 1268 | COMPASS E6 | |
| 1310 | Aeronautical radar | |
| 1317 | Aeronautical radar | |
| 1330 | Aeronautical radar | |
| 1337 | Aeronautical radar | |
| 1376-1386 | GPS L3 | Intermittent |
| 1525-1564 | INMARSAT satellites | |
| 1564-1584 | GPS L1 | Very strong |
| 1598-1609 | GLONASS L1 | |
| 1618-1627 | IRIDIUM satellites | |
| 1642 | 2nd harmonic VLA radios | Sporadic |
| 1683-1687 | GOES weather satellite | |
| 1689-1693 | GOES weather satellite | |
| 1700-1702 | NOAA weather satellite | |
| 1705-1709 | NOAA weather satellite | |
| 1930-1990 | PCS cell phone base stations | |
| 2178-2195 | Satellite Downlink | very strong* |
| 2320-2350 | Sirius/XM Satellite radio | very strong* |
| 3700-4200 | Satellite Downlinks | very strong* |
The three last entries in the table deserve extra discussion. These are all satellite transmissions, whose severity is a strong function of the angular offset between the particular satellite and the antenna. It appears that significant degradation can occur if the antennas are within ~10 degrees of the satellite. The great majority of the satellites are along the 'Clarke Belt' -- the zone of geosynchronous satellites. As seen from the VLA, this belt is at a declination of about -5.5 degrees. There are dozens -- probably hundreds -- of satellites 'parked' along this belt, transmitting in many bands: S, C, Ku, K, and Ka at a minimum. Observations of sources in the declination rate of +5 to -15 degrees can expect to be significantly degraded due to satellite transmission. The Sirius digital radio system (and probably the satellites in the 2178 -- 2195 MHz band) comprises three satellites in a 24-hour, high eccentricity orbit with the apogee above the central U.S. For the Sirius system, the orbit is arranged such that each of the three satellites spends about eight hours near an azimuth of 25 degrees and an elevation of 65 degrees. The corresponding region in astronomical coordinates is between declinations 50 to 65 degrees, and hour angles between -1 and -2 hours. Observations at S-band within that area may -- or may not -- be seriously affected. The most reliable way to judge the seriousness of the satellite emissions is to inspect the switched power table data, particularly in those subbands where there is little RFI.
VLA staff periodically observes the entire radio spectrum, with the VLA, from 1.0 through 50.0 GHz with 125 kHz channel resolution to monitor the ever-changing RFI spectrum. Plots from this program, accompanied with tables of identified sources are available online, at https://science.nrao.edu/facilities/vla/docs/manuals/obsguide/modes/rfi. Users concerned about the precise frequencies of strong RFI, and the likelihood of being affected, are encouraged to peruse these plots.
Although most of the stronger sources of RFI are always present, it is very difficult to reliably predict their effect on observations. Besides the already noted dependence on frequency and array configuration, there is another significant dependency on sky location for those satellites in geostationary orbit. For these transmitters, (for example, the frequency range from 3.8 to 4.2 GHz), the effect on observing varies dramatically on the declination of the target source. Sources near zero declination will be very strongly affected, while observations north of the zenith may well be nearly unaffected, especially at the highest resolutions.
Also available are total-power plots of all RFI observations made by the interference protection group, from 1993 onwards at http://www.vla.nrao.edu/cgi-bin/rfi.cgi. For general information about the RFI environment, contact the head of the IPG (Interference Protection Group) by sending e-mail to nrao-rfi@nrao.edu.
The VLA electronics (including the WIDAR correlator) have been designed to minimize gain compression due to very strong RFI signals, so that in general it is possible to observe in spectral windows containing RFI, provided the spectra are well sampled to constrain Gibbs ringing, and spectral smoothing (such as Hanning) is applied. Both AIPS and CASA provide useful tasks which automatically detect and flag spectral channels/times which contain strong RFI.
Extracting astronomy data from frequency channels in which the RFI is present is much more difficult. Testing of algorithms which can distinguish and subtract RFI signals from interferometer data is ongoing.
The 3-bit samplers will be more susceptible to RFI signals than the 8-bit samplers, since the latter have more 'levels' within which these strong signals can be accommodated. However, since the RFI power at the bands where the 3-bit samplers will most commonly be used (C, X, Ku, K, Ka, and Q) is nearly always less than the total noise power, we do not expect problems when wide-band 3-bit observing is done in these bands.
Calibration of VLA data when strong RFI is present within a subband can be difficult. Careful editing of the data, using newly available programs within CASA and AIPS, will be necessary before sensible calibration can be done. The use of spectral smoothing (typically, Hanning), prior to editing and calibration, is strongly recommended when RFI is present within a subband.
Identification and removal of RFI is always more effective when the spectral and temporal resolutions are high. However, the cost of higher spectral and temporal resolution is in database size and, especially, in computing time. A good strategy is to observe with high resolution, then average down in time and frequency once the editing is completed.
Subarrays
The continuum subarray option offers two 1 GHz baseband pairs (two 8-bit baseband pairs, each with 1 GHz in RCP and 1 GHz in LCP) in up to 3 subarrays, with the same spectral channel and polarization product options as are available for wideband observing. The setup for each subarray is completely independent, in terms of observing frequency, polarization products, and integration times.
When using three subarrays, there are some restrictions on the number of antennas in each subarray. The Baseline Board in the correlator treats each set of 4 antennas independently, using a separate column of correlator chips. With 8 such columns, the correlator can handle up to 8x4= 32 antennas. The correlator configuration software requires that a given column not be split across subarrays. This does not matter when using only two subarrays, but forces some subtle restrictions when using three. For instance, one cannot observe with 9 antennas in each of 3 subarrays, because 9 antennas requires three columns (two with 4 antennas each, and one with 1 antenna); three subarrays of 9 antennas each would require 3x3= 9 columns, one more than are actually available. Splitting the array into 10, 9, and 8 antennas is allowed, since the first two subarrays use 3 columns each, while the third uses only two.
The following table gives four examples of how correlator resources can be split into multiple subarrays. Antennas in each subarray are color-coded: red for subarray 1, green for subarray 2 (if present), and blue for subarray 3 (if present). The last column gives the number of antennas in each subarray (e.g., in the setup shown in the first row, subarray 1 has 10 antennas; subarray 2 has 9 antennas; and subarray 3 has 8 antennas). In all cases a total of 27 antennas are used. [The columns are numbered in reverse order (C7 to C0) to match the numbering scheme used on the actual Baseline Boards.]
| Some Possible Subarray Options | ||||||||
|---|---|---|---|---|---|---|---|---|
| Number of antennas correlated using each Baseline Board column | Number | |||||||
| C7 | C6 | C5 | C4 | C3 | C2 | C1 | C0 | of antennas |
| 4 | 4 | 2 | 4 | 4 | 1 | 4 | 4 | 10 + 9 + 8 |
| 4 | 4 | 4 | 2 | 4 | 4 | 4 | 1 | 14 + 13 |
| 4 | 4 | 3 | 4 | 4 | 3 | 3 | 2 | 11 + 11 + 5 |
| 4 | 4 | 4 | 4 | 4 | 4 | 3 | -- | 27 |
Positional Accuracy & Astrometry
In preparation for observing, the a-priori position must be known to within the antenna primary beam, except perhaps for mosaicing observations. In the special case of using the phased VLA as a VLBI element , the a-priori position must be accurate to within the synthesized beam of the array.
In post-processing, target positions are typically determined from an image made after phase calibration, i.e. correcting the antenna and atmospheric phases as determined on the reference source. The accuracy of the calibration determines the accuracy of the positions in the image. (Note that phase self-calibration imposes the assumed position of the model, i.e., makes the position indeterminate. Therefore, an absolute position cannot be determined after self-calibration, but relative positions between features within a self-calibrated image are valid.)
It may help to think of astrometry in 2 steps, narrow and wide-field.
In narrow-field astrometry, the target is close to the phase tracking center and the antennas nod every few minutes between the target and a calibrator. Under good conditions of phase stability, accurate antenna positions, (so-called 'baselines'), a strong target, a close calibrator with accurately known position, and rapid switching, the accuracy can approach 1-2% of the synthesized beam, with a floor of ~2 mas. Even under more typical conditions, 10% of the beam is readily achieved.
Astrometric calibrators are marked 'J2000 A' in the VLA calibrator list, and have an accuracy of ~2 mas. Other catalogs from the USNO and the VLBA are also useful, but offsets may exist between the VLA and VLBA centroids, arising from extended structure in the particular source, and the different resolutions of the arrays.
For studies of proper motion and parallax, the absolute accuracy of a calibrator may be less important than its stability over time. Close or in-beam calibrators with poor a-priori positions can be used, and tied to the ICRF reference frame in the same or separate observations.
Phase stability can be assessed in real time from the Atmospheric Phase Interferometer (API) at the VLA site, which uses observations of a geostationary satellite at ~12GHz. Dynamic scheduling uses the API data to run a project under suitable conditions, specified by the user. Note that VLBI projects using the phased VLA will typically be fixed date, not dynamically scheduled.
The widefield case is to determine the positions of targets within the primary beam, referenced to a calibrator within the beam or close by. In addition to the previous effects, there are distortions as a function of position in the field, from small errors in the Earth orientation parameters (EOP) used at correlation time, differential aberration, and phase gradients across the primary beam. With no special effort, the errors build up to roughly ~1 synthesized beam at a separation of ~10^4 beams from the phase tracking center. Not all these errors are fully understood, and accurate recovery of positions over the full primary beam in the wideband, widefield case is a research area. These effects are handled somewhat differently in the post-processing packages, the current situation is described below. Improvements are in progress, check with EVLA staff.
The dominant widefield effects are differential aberration and EOP errors. Data exported from the EVLA archive as a CASA measurement set will have reasonably accurate EOP attached by the CASA FILLER, based on BIPM values pertaining to the observation date, but determined after the fact, on the date of export. These EOP differ slightly from those used at correlation (observation) time, when only predictions are available. The difference is usually negligible. However, CASA (program FIXVIS) does not, as of June 2013, correct for the differential aberration. On the other hand, AIPS corrects differential aberration (program UVFIX), but, because there is no EOP data in the archived ASDM, the UVFITS file imported by BDF2AIPS has zeros in the antenna table where the EOP should be. One can edit in the EOP and proceed with UVFIX, but it is better that the ASDM stores EOP in the first place. This feature is expected by late 2013. The capabilities of both CASA and AIPS should be equivalent in this regard by 2014.
Limitations on Imaging Performance
Image Fidelity
Image fidelity is a measure of the accuracy of the reconstructed sky brightness distribution. A related metric, dynamic range, is a measure of the degree to which imaging artifacts around strong sources are suppressed, which in turn implies a higher fidelity of the on-source reconstruction.
With conventional external calibration methods, even under the best observing conditions, the achieved dynamic range will rarely exceed a few hundred. The limiting factor is most often the effective phase stability of the telescope due to atmospheric/ionospheric fluctuations, although pointing errors and changes in atmospheric opacity can also be a limiting factor. If a good model of the sky brightness distribution exist (e.g. use of compact structures of sufficient strength, though a good model of resolved sources in the field of view may also be used), standard self-calibration can be counted on to improve the images. At low frequencies where the dominant phase error is due to ionospheric plasma density fluctuations, more advanced techniques may be required to account for change of ionospheric phase across the field of view. Dynamic ranges in the thousands to hundreds of thousands can be achieved using these techniques, depending on the underlying nature of the errors. With the new WIDAR correlator and its much greater bandwidths and much higher sensitivities, self-calibration methods can be extended to observations of sources with much lower flux densities than very possible with the old VLA.
The choice of image reconstruction algorithm also affects the correctness of the on-source brightness distribution. The CLEAN algorithm is most appropriate for predominantly point-source dominated fields. Extended structure is better reconstructed with multi-resolution and multi-scale algorithms. For high dynamic ranges with wide bandwidths, algorithms that model the sky spectrum as well as the average intensity can yield more accurate reconstructions.
Invisible Structures
An interferometric array acts as a spatial filter, so that for any given configuration, structures on a scale larger than the fringe spacing of the shortest baseline will be completely absent. Diagnostics of this effect include negative bowls around extended objects, and large-scale stripes in the image. Image reconstruction algorithms such as multi-resolution and multi-scale CLEAN can help to reduce or eliminate these negative bowls, but care must be taken in choosing appropriate scale sizes to work with.
Table 5 gives the largest scale visible to each configuration/band combination.
Poorly Sampled Fourier Plane
Unmeasured Fourier components are assigned values by the deconvolution algorithm. While this often works well, sometimes it fails noticeably. The symptoms depend upon the actual deconvolution algorithm used. For the CLEAN algorithm, the tell-tale sign is a fine mottling on the scale of the synthesized beam, which sometimes even organizes itself into coherent stripes. Further details are to be found in Reference 1 in Documentation.
Sidelobes from non-Deconvolved Sources
At the lower frequencies, large numbers of detectable background sources are located throughout the primary antenna beam, and into its first sidelobe. Sidelobes from those sources which have not been deconvolved will lower the image quality of the target source. Although bandwidth smearing and time-averaging will tend to reduce the effects of these sources, the very best images will require careful imaging of all significant background sources. The deconvolution tasks in AIPS (IMAGR) and CASA (clean) are well suited to this task. Sidelobe confusion is a strong function of observing band -- affecting most strongly L and P-band observations. It is rarely a significant problem for observations at frequencies above 4 GHz.
Sidelobes from Strong Sources
An extension of the previous section is to very strong sources located anywhere in the sky, such as the Sun (especially when a flare is active), or when observing with a few tens of degrees of the very strong sources Cygnus A and Casseopeia A. Image degradation is especially notable at lower frequencies, shorter configurations, and when using narrow-bandwidth observations (especially in spectral line work) where chromatic aberration cannot be utilized to reduce the disturbances. In general, the only relief is to include the disturbing sources in the imaging, or to observe when these objects are not in the viewable hemisphere.
Wide-band Imaging
The very wide bandpasses provided by the Jansky Very Large Array enable imaging over 2:1 bandwidth ratios -- at L, S, and C bands, the upper frequency is twice that of the lower frequency. It is this wide bandwidth which enables sub-microJy sensitivity.
In many cases, where the observation goal is a simple detection, and there are no strong sources near to the region of interest, standard imaging methods that combine the data from all frequencies into one single image (multi-frequency-synthesis) may suffice. This is because the wide-band system makes a much better synthesized beam -- especially for longer integrations -- than the old single-frequency beam, thus considerably reducing the region of sky which is affected by incorrect imaging/deconvolution. A rough rule of thumb is that -- provided a strong source is not adjacent to the target zone -- if the necessary dynamic range in the image is less than 1000:1, (i.e., the strongest source in the beam is less than 1000 times higher than the noise), a simple wide-band map may suffice.
For higher dynamic ranges, complications arise from the fact that the brightness in the field of view dramatically changes as a function of frequency, both due to differing structures in the actual sources in the field of view, and due to the attenuation of the sources by the primary beam. One symptom of such problems is the appearance of radial spokes around bright sources, visible above the noise floor, when imaged as described above.
The simplest solution is to simply make a number of maps (say, one for each subband), which can then be suitably combined after correction for the primary beam shape. But with up to 64 subbands available with the VLA's new correlator, this is not always the optimal approach. Further, images at all bands must be smoothed to the angular resolution at the lowest frequency before any spectral information can be extracted, and with a 2:1 bandwidth the difference in angular resolution across the band will be significant.
A better approach is to process all subbands simultaneously, utilizing software which takes into account the possibility of spatially variant spectral index and curvature, and knows the instrumentally-imposed attenuation due to the primary beam. Such wideband imaging algorithms are now available within CASA as part of the clean task, and work is under way to integrate them fully with wide-field imaging techniques.
Wide Field Imaging
Wide-field observing refers primarily to the non-coplanar nature of the VLA when observing in non-snapshot mode. At high angular resolutions and low frequencies, standard imaging methods will produce artifacts around sources away from the phase center. Faceted imaging (AIPS, CASA) and w-projection (CASA) techniques can be used to solve this problem.
Another aspect of wide-field observing is the accurate representation of primary beam patterns, and their use during imaging. This is relevant only for very high dynamic ranges ( > 10000 ) or when there are very strong confusing sources at and beyond the half-power point of the primary beam. This problem is worse with a wide-band instrument simply because the size of the primary beam (and the radius at which the half-power point occurs) varies with frequency, while there is also increased sensitivity out to a wider field of view. Work is under way to commission algorithms that deal with these effects by modeling and correcting for frequency-dependent and rotating primary beams per antenna, during imaging. Please note, however, that most advanced methods will lead to a significant increase in processing time, and may not always be required. Therefore, in the interest of practicality, they should be used only if there is evidence of artifacts without these methods.
Finally, all of the above effects come into play for mosaicing, another form of wide-field imaging in which data from multiple pointings are combined during or after imaging.
Calibration and Flux Density Scale
The VLA Calibrator List contains information on 1860 sources sufficiently unresolved and bright to permit their use as calibrators, and is also available within the Observation Preparation Tool.
Accurate flux densities can be obtained by observing one of 3C286, 3C147, 3C48 or 3C138 during the observing run. Not all of these are suitable for every observing band and configuration - consult the VLA Calibrator Manual for advice. Over the last several years, we have implemented accurate source models directly in AIPS and CASA for much improved calibration of the amplitude scales. Models are available for 3C48, 3C138, 3C147, and 3C286 for L, C, X, Ku, K, and Q bands. At Ka band either of the K or Q band models works reasonably well. For S-band, use the L or C band models.
Since the standard source flux densities are slowly variable, we monitor their flux densities when the array is in its D configuration. As the VLA cannot accurately measure absolute flux densities, the values obtained must be referenced to assumed or calculated standards, as described in the next paragraph. Table 11 shows the flux densities of these sources in January 2012 at the standard VLA bands. The flux density scale for the VLA, from 1 through 50 GHz, is based on emission models of the planet Mars, which is then calibrated to the CMB dipole using WMAP (Wilkinson Microwave Anisotropy Probe) observations (see Perley and Butler, 2013, for details). The source 3C286 (=J1331+3030) is known to be non-variable, and has thus been adopted as the prime flux density calibrator source for the VLA. The adopted polynomial expression for the spectral flux density for 3C286 is:
\[\log(S) = 1.2515 - 0.4605 \log(f) - 0.1715 \log^2(f) + 0.0336 \log^3(f)\]
where S is the flux density in Jy, and f is the frequency in GHz.
The absolute accuracy of our flux density scale is estimated to be about 2%. With care, the internal accuracy in flux density bootstrapping is better than 1% at all bands except Q-band, where pointing errors limit bootstrap accuracy to perhaps 3%. Note that such high internal accuracies are only possible in long-duration observations where the antenna gains curves and atmospheric opacity can be directly measured, and where there is good elevation overlap between the target source(s) and the flux density standard calibrator.
| Source | 1465 | 2565 | 4885 | 8435 | 14965 | 22460 | 36435 | 43340 |
|---|---|---|---|---|---|---|---|---|
| 3C48 = J0137+3309 | 15.56 | 9.80 | 5.39 | 3.14 | 1.77 | 1.19 | 0.73 | 0.63 |
| 3C138 = J0521+1638 | 8.71 | 6.17 | 4.02 | 2.78 | 1.89 | 1.46 | 1.03 | 0.92 |
| 3C147 = J0542+4951 | 21.85 | 13.75 | 7.59 | 4.49 | 2.59 | 1.77 | 1.10 | 0.94 |
| 3C286 = J1331+3030 | 14.90 | 10.03 | 7.34 | 5.09 | 3.39 | 2.52 | 1.75 | 1.53 |
| 3C295 = J1411+5212 | 22.15 | 12.95 | 6.41 | 3.34 | 1.62 | 0.957 | 0.507 | 0.403 |
| NGC7027 | 1.62 | 3.59 | 5.38 | 5.79 | 5.62 | 5.42 | 5.18 | 5.04 |
The sources 3C48, 3C147, and 3C138 are all slowly variable. VLA staff monitor these variations on timescale of a year or two, and suitable polynomial coefficients are determined for them which should allow accurate flux density bootstrapping. These coefficients are updated approximately every other year, and are used in the AIPS task SETJY and in the CASA task setjy.
The VLA antennas have elevation-dependent gain variations which are important to account for at the four highest-frequency bands. Gain curves are determined by VLA staff approximately every other year, and the necessary corrections are applied to the visibility data when these data are downloaded from the archive. In addition to this, atmospheric opacity will also cause an elevation-dependent gain which is particularly notable at these four highest frequency bands. At the current time, we do not have an atmospheric opacity monitoring procedure, so users should utilize the appropriate tasks available in both AIPS and CASA to estimate and correct for the opacity using ground-based weather data. Correction of these gain dependencies, plus regular calibration using a nearby phase calibrator, should enable good amplitude gain calibration for most users. Note that extraordinary attenuation by clouds can only be (approximately) corrected for by regular observation of a nearby calibrator.
A better procedure for removing elevation gain dependencies uses the AIPS task ELINT. This task will generate a 2nd order polynomial gain correction utilizing your own calibrator observations. This will remove both the antenna and opacity gain variations, and has the decided advantage of not utilizing opacity models or possibly outdated antenna gain curves. Use of this procedure is only practical if your observations span a wide range in elevation.
By far the most important gain variation effect is that due to pointing. Daytime observations on sunny days can suffer pointing errors of up to one arcminute (primarily in elevation). This effect can be largely removed by utilizing the 'referenced pointing' procedure. This determines the pointing offset of a nearby calibrator, which is then applied to subsequent target source observations. It is recommended that this local offset be determined at least hourly, utilizing an object within 15 degrees of the target source -- preferentially at an earlier HA. Studies show that the maximum pointing error will be reduced to about 7 arcseconds, or better. VLA staff continue to work on improving this essential methodology.
The VLA's post-amplifiers are not temperature stabilized, and exhibit significant gain changes between night and day, particularly at the four highest frequency bands. Changes as large as 30% have been seen between night and day in calm, clear conditions! These gain changes (and others caused by possible changes in attenuator settings) are monitored and will be removed with excellent accuracy by application of the internal calibration signal, whose results are recorded in the switched power table (SY table, in AIPSese). These corrections are not applied by default -- users who wish to correct for these gain changes must utilize the appropriate tasks in AIPS or CASA. For the most accurate flux density bootstrapping, this table must be applied to the visibility data before calibration. Gain bootstrapping better than 1% can be accomplished for the 8-bit sampler system after application of the SY table data. For the 3-bit system there is an additional complication, as the values of the SY data are sensitive to the total power, as well as the system gain. VLA staff are currently working on a methodology to remove the total power dependency. Not applying the SY table data will reduce bootstrapping accuracy to perhaps 10%, and possibly worse, if the observation of the flux density calibrator is not close in time to the local phase/amplitude cailbrator.
Complex Gain Calibration
General Guidelines for Gain Calibration
Adequate gain calibration is a complicated function of source-calibrator separation, frequency, array scale, and weather. And, since what defines adequate for some experiments is completely inadequate for others, it is difficult to define simple guidelines to ensure adequate phase calibration in general. However, some general statements remain valid most of the time. These are given below.
- Tropospheric effects dominate at wavelengths shorter than 20 cm, ionospheric effects dominate at wavelengths longer than 20 cm.
- Atmospheric (troposphere and ionosphere) effects are nearly always unimportant in the C and D configurations at L and S bands, and in the D configuration at X and C bands. Hence, for these cases, calibration need only be done to track instrumental changes - a couple of times per hour is generally sufficient.
- If your target object has sufficient flux density to permit phase self-calibration, there is no need to calibrate more than once hourly at low frequencies (L/S/C bands) or 15 minutes at high frequencies (K/Ka/Q bands) in order to track pointing or other effects that might influence the amplitude scale. The newly-enhanced sensitivity of the VLA now guarantees, for full-band continuum observations, that every field will have enough background sources to enable phase self-calibration at L and S bands, and probably also at C-band. At higher frequencies, the background sky is not sufficient, and only the flux of the target source itself will be available.
- The smaller the source-calibrator angular separation, the better. In deciding between a nearby calibrator with an "S" code in the calibrator database, and a more distant calibrator with a "P" code, the nearby calibrator is usually the better choice. A detailed description of calibrator codes is available in the Key to the calibrator list.
- In clear and calm conditions, most notably in the summer, phase stability often deteriorates dramatically after about 10AM, due to small-scale convective cells set up by solar heating. Observers should consider a more rapid calibration cycle for observations between this time and a couple hours after sundown.
- At high frequencies, and longer configurations, rapid switching between the source and nearby calibrator is often helpful. See Rapid Phase Calibration and the Atmospheric Phase Interferometer (API).
- Use Figure 1 below to estimate how much time is minimally needed for each gain calibrator scan. For instance, a 1 Jy calibrator and 4 MHz total bandwidth requires at least 30 seconds on source
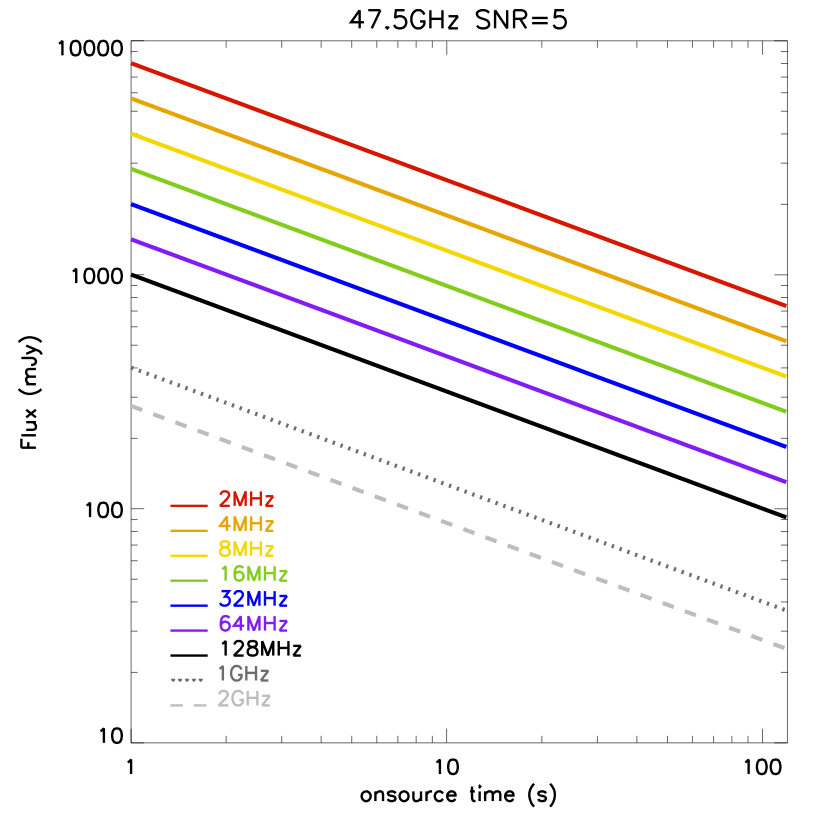
Figure 1 - minimum time required on a gain calibrator scan as a function of bandwidth and calibrator flux for the rather extreme case of upper Q-band. Durations derived from this plot will definitely be sufficient for all other bands.
Rapid Phase Calibration and the Atmospheric Phase Interferometer (API)
For some objects, and under suitable weather conditions, the phase calibration can be considerably improved by rapidly switching between the source and calibrator. Source-Calibrator observing cycles as short as 40 seconds can be used for very small source-calibrator separations. However, observing efficiency declines for very short cycle times, so it is important to balance this loss against a realistic estimate of the possible gain. Experience has shown that cycle times of 100 to 150 seconds at high frequencies have been effective for source-calibrator separations of less than 10 degrees. For the old VLA this was known as "fast-switching." For the upgraded VLA it is just a loop of source-calibrator scans with short scan length. This technique "stops" tropospheric phase variations at an "effective" baseline length of ∼vat/2 where va is the atmospheric wind velocity aloft (typically 10 to 15 m/sec), and t is the total switching time. It has been demonstrated to result in images of faint sources with diffraction-limited spatial resolution on the longest VLA baselines. Under average weather conditions, and using a 120 second cycle time, the residual phase at 43 GHz should be reduced to ≤ 30 degrees. Note, however, that for the compact D-configuration, and a typical wind velocity, this "effective" baseline length is the same as, or larger than, the longest baseline in the array, and it is not worth the increased overhead of short cycle times. Under these circumstances it is sufficient to calibrate every 5-10 minutes to track the instrumental changes. The fast switching technique will also not work in bad weather (such as rain showers, or when there are well-developed convection cells - most notably, thunderstorms). It is also important to specify correctly the required tropospheric phase stability as measured by the Atmospheric Phase Interferometer at observe time (see below).
Further details can be found in VLA Scientific Memos # 169 and 173 (http://www.vla.nrao.edu/memos/sci/). These memos, and other useful information, can be obtained from References 9 and 10 in Documentation. See also the High Frequency Observing guide for additional recommendations on observing at high frequencies.
An Atmospheric Phase Interferometer (API) is used to continuously measure the tropospheric contribution to the interferometric phase using an interferometer comprising two 1.5 meter antennas separated by 300 meters, observing an 11.7 GHz beacon from a geostationary satellite. The API data can be used to estimate the required calibration cycle times when using fast switching phase calibration, and in the worst case, to indicate to the observer that high frequency observing may not be possible with current weather conditions.
Characteristic seasonal averages are represented below:
| Month | API (night) [deg] | API (median) [deg] | API (day) [deg] | Wind (night) [m/s] | Wind (median) [m/s] | Wind (day) [m/s] |
|---|---|---|---|---|---|---|
| January | 2.3 | 2.8 | 3.6 | 1.6 | 1.9 | 2.3 |
| February | 2.9 | 3.4 | 4.5 | 4.0 | 4.3 | 4.5 |
| March | 2.8 | 3.7 | 5.5 | 3.4 | 3.9 | 4.7 |
| April | 3.3 | 4.5 | 6.2 | 5.3 | 5.5 | 5.8 |
| May | 2.9 | 4.6 | 6.7 | 2.6 | 3.2 | 3.7 |
| June | 3.8 | 5.5 | 7.4 | 2.5 | 3.9 | 6.3 |
| July | 6.2 | 8.3 | 10.5 | 2.9 | 2.9 | 3.0 |
| August | 5.4 | 7.1 | 11.3 | 1.7 | 2.3 | 3.0 |
| September | 5.2 | 6.6 | 8.8 | 2.3 | 3.0 | 3.6 |
| October | 4.2 | 5.3 | 7.4 | 2.3 | 2.9 | 3.7 |
| November | 2.6 | 3.0 | 4.0 | 1.2 | 2.5 | 1.6 |
| December | 2.8 | 3.2 | 4.1 | 1.2 | 1.6 | 2.7 |
- Note: day indicates sunrise to sunset values; night indicates sunset to sunrise values.
Polarization
For projects requiring imaging in Stokes Q and U, the instrumental polarization should be determined through observations of a bright calibrator source spread over a range in parallactic angle. The phase calibrator chosen for the observations can also double as a polarization calibrator provided it is at a declination where it moves through enough parallactic angle during the observation (roughly Dec 15deg to 50deg for a few hour track). The minimum condition that will enable accurate polarization calibration from a polarized source (in particular with unknown polarization) is three observations of a bright source spanning at least 60 degrees in parallactic angle (if possible schedule four scans in case one is lost). If a bright unpolarized unresolved source is available (and known to have very low polarization) then a single scan will suffice to determine the leakage terms. The accuracy of polarization calibration is generally better than 0.5% for objects small compared to the antenna beam size. At least one observation of 3C286 or 3C138 is required to fix the absolute position angle of polarized emission. 3C48 also can be used for this at frequencies of ~3 GHz and higher, or 3C147 at frequencies abover ~10 GHz. The table below shows the measured fractional polarization and intrinsic angle for the linearly polarized emission for these four sources in December 2010. Note that 3C138 is variable -- the polarization properties are known to be changing significantly over time, most notably at the higher frequencies. See Perley and Butler (2013b) for details.
More information on polarization calibration strategy can be found in the VLA Observing Guide.
| Freq. | 3C48Pol | 3C48Ang | 3C138Pol | 3C138Ang | 3C147Pol | 3C147Ang | 3C286Pol | 3C286Ang |
|---|---|---|---|---|---|---|---|---|
| GHz | % | Deg. | % | Deg. | % | Deg. | % | Deg. |
| 1.05 | 0.3 | 25 | 5.6 | -14 | <.05 | - | 8.6 | 33 |
| 1.45 | 0.5 | 140 | 7.5 | -11 | <.05 | - | 9.5 | 33 |
| 1.64 | 0.7 | -5 | 8.4 | -10 | <.04 | - | 9.9 | 33 |
| 1.95 | 0.9 | -150 | 9.0 | -10 | <.04 | - | 10.1 | 33 |
| 2.45 | 1.4 | -120 | 10.4 | -9 | <.05 | - | 10.5 | 33 |
| 2.95 | 2.0 | -100 | 10.7 | -10 | <.05 | - | 10.8 | 33 |
| 3.25 | 2.5 | -92 | 10.0 | -10 | <.05 | - | 10.9 |
33 |
| 3.75 | 3.2 | -84 | - | - | <.04 | - | 11.1 | 33 |
| 4.50 | 3.8 | -75 | 10.0 | -11 | 0.1 | -100 | 11.3 | 33 |
| 5.00 | 4.2 | -72 | 10.4 | -11 | 0.3 | 0 | 11.4 | 33 |
| 6.50 | 5.2 | -68 | 9.8 | -12 | 0.3 | -65 | 11.6 | 33 |
| 7.25 | 5.2 | -67 | 10.0 | -12 | 0.6 | -39 | 11.7 | 33 |
| 8.10 | 5.3 | -64 | 10.4 | -10 | 0.7 | -24 | 11.9 | 34 |
| 8.80 | 5.4 | -62 | 10.1 | -8 | 0.8 | -11 | 11.9 | 34 |
| 12.8 | 6.0 | -62 | 8.4 | -7 | 2.2 | 43 | 11.9 | 34 |
| 13.7 | 6.1 | -62 | 7.9 | -7 | 2.4 | 48 | 11.9 | 34 |
| 14.6 | 6.4 | -63 | 7.7 | -8 | 2.7 | 53 | 12.1 | 34 |
| 15.5 | 6.4 | -64 | 7.4 | -9 | 2.9 | 59 | 12.2 | 34 |
| 18.1 | 6.9 | -66 | 6.7 | -12 | 3.4 | 67 | 12.5 | 34 |
| 19.0 | 7.1 | -67 | 6.5 | -13 | 3.5 | 68 | 12.5 | 35 |
| 22.4 | 7.7 | -70 | 6.7 | -16 | 3.8 | 75 | 12.6 | 35 |
| 23.3 | 7.8 | -70 | 6.6 | -17 | 3.8 | 76 | 12.6 | 35 |
| 36.5 | 7.4 | -77 | 6.6 | -24 | 4.4 | 85 | 13.1 | 36 |
| 43.5 | 7.5 | -85 | 6.5 | -27 | 5.2 | 86 | 13.2 | 36 |
High sensitivity linear polarization imaging may be limited by time dependent instrumental polarization, which can add low levels of spurious polarization near features seen in total intensity and can scatter flux throughout the polarization image, potentially limiting the dynamic range. Preliminary investigation of the EVLA's new polarizers indicates that these are extremely stable over the duration of any single observation, strongly suggesting that high quality polarimetry over the full bandwidth will be possible.
The accuracy of wide field linear polarization imaging will be limited, likely at the level of a few percent at the antenna half-power width, by angular variations in the antenna polarization response. Algorithms to enable removable of this angle-dependent polarization are being tested, and observations to determine the antenna polarizations have begun. Circular polarization measurements will be limited by the beam squint, due to the offset secondary focus feeds, which separates the RCP and LCP beams by a few percent of the FWHM. The same algorithms noted above to correct for antenna-induced linear polarization can be applied to correct for the circular beam squint. Measurement of the beam squints, and testing of the algorithms, is ongoing.
Ionospheric Faraday rotation of the astronomical signal is always notable at 20 cm. The typical daily maximum rotation measure under quiet solar conditions is 1 or 2 radians/m2, so the ionospherically-induced rotation of the plane of polarization at these bands is not excessive - 5 degrees at 20 cm. However, under active conditions, this rotation can be many times larger, sufficiently large that polarimetry is impossible at 20 cm with corrrection for this effect. The AIPS program TECOR has been shown to be quite effective in removing large-scale ionospherically induced Faraday Rotation. It uses currently-available data in IONEX format. Please consult the TECOR help file for detailed information.
VLBI Observations
The VLA can now participate in VLBI observations with the VLBA. Currently, this is only allowed in phased array mode (single dish is only available through the VLBA Resident Shared Risk Observing program) with restricted WIDAR correlator configurations. For more details see the VLBI at the VLA documentation. In phased array mode the program TelCal derives the antenna-based delay and phase corrections needed for antenna phasing in real time. This correction is applied to the antenna signals before they are summed, requantized to 2-bits, and recorded in VDIF format on the Mark5C disk at the VLA site. The disk(s) are then transported to Socorro, NM and correlated on the DiFX correlator with other VLBI stations which participated in the observation. Standard VLA data, i.e., correlations between VLA antennas, are also archived in the NRAO science data archive.
Snapshots
The two-dimensional geometry of the VLA allows a snapshot mode whereby short observations can be used to image relatively bright unconfused sources. This mode is ideal for survey work where the sensitivity requirements are modest.
Single snapshots with good phase stability of strong sources should give dynamic ranges of a few hundred. Note that because the snapshot synthesized beam contains high sidelobes, the effects of background confusing sources are much worse than for full syntheses, especially at 20 cm in the D configuration, for which a single snapshot will give a limiting noise of about 0.2 mJy. This level can be reduced by taking multiple snapshots separated by at least one hour. Use of the AIPS program 'IMAGR' or CASA task 'clean' is necessary to remove the effects of background sources. Before considering snapshot observations at 20 cm, users should first determine if the goals desired can be achieved with the existing "Faint Images of the Radio Sky at Twenty-centimeters survey(FIRST, http://www.cv.nrao.edu/first/)" (B configuration) or the "Co-Ordinated Radio 'N' Infrared Survey for High-mass star formation (CORNISH, http://cornish.leeds.ac.uk/public/index.php)" (B configuration), or the NRAO VLA Sky Survey (NVSS, http://www.cv.nrao.edu/nvss/) (D configuration, all-sky) surveys.
Shadowing and Cross-Talk
Observations at low elevation in the C and D configurations will commonly be affected by shadowing. It is strongly recommended that all data from a shadowed antenna be discarded. This will automatically be done during filling (CASA task importasdm) when using the default inputs (Note: For archival VLA data, the AIPS task FILLM can also flag based on shadowing). AIPS task UVFLG can be used to flag modern VLA data based on shadowing as well, although it will only flag based on antennas in the dataset, and is ignorant of antennas in other sub-arrays.
Cross-talk is an effect in which signals from one antenna are picked up by an adjacent antenna, causing an erroneous correlation. This effect is important at low frequencies in compact configurations. Careful examination of the visibilities is necessary to identify and remove this form of interference.
Combining Configurations and Mosaicking
Any single VLA configuration will allow accurate imaging of a range of spatial scales determined by the shortest and longest baselines. For extended and structured objects, it may be required to obtain observations in multiple array configurations. It is advisable that the frequencies used be the same for all configurations to be combined. The ideal combination of arrays results in a uv-plane with all cells equally filled by uv-points. To first order, this can be achieved by using the beam sizes of the individual arrays to inversely scale the on-source integration time. This approach is equivalent to achieving the same surface brightness sensitivity for all arrays on all scales. For the VLA, observations in the different configurations generate beam sizes that decrease by factors of 3, i.e. C configuration generates a 3 times smaller beam than D configuration, B 3 times smaller than C, and A three times smaller than B. Thus, on-source integrations would increase by about an order of magnitude between each array. Such a drastic increase is very expensive and, in fact, not necessary since some spatial scales are common to more than a single array, which is equivalent to some uv-cells being filled more than others. The best way to fill the uv plane depends on many factors, such as declination of the source, LST time of the observation, and bandwidth.
For the VLA, experience shows that a factor of about 3 in on-source integration time for the different array configurations works well for most experiments.
E.g., 20min on-source time in D, 1h in C, 3h in B, and 9h in A should produce a decent map. Using large bandwidths and multi-frequency synthesis will broaden all uv tracks radially and one may need even less array configurations or shorter integration times between the different arrays.
Objects larger than the primary antenna pattern may be mapped through the technique of interferometric mosaicking. The VLA has no limit on the number of pointings for each mosaic. Typically hexagonal, rectangular, or individual pointing patterns are used and the overlap regions will result in an improved rms over each individual pointing. Given the many, potentially short observations, it is important to obey the data rate limits outlined in the Time Resolution and Data Rates Section.
As of Semester 2015A on-the-fly mosaics, i.e. dumping the data while moving the telescopes across the source, is available as Shared Risk Observing.
Time-variable structures (such as the nuclei of radio galaxies and quasars) cause special, but manageable, problems. See the article by Mark Holdaway in reference 2 (Documentation) for more information.
Guidelines for mosaicking with the VLA are given in the VLA Observing Guide.
Pulsar Observing
The VLA can now be used for two kinds of pulsar observing: phase-binning using the WIDAR correlator, and using the phased-array for pulsar dedispersion (either search or fold mode). Either of these types of observing are considered Resident Shared Risk (RSRO), and close collaboration with NRAO staff is required for their use.




Connect with NRAO