Sensitivity

The theoretical thermal noise expected for an image using natural weighting of the visibility data is given by:

 

\[\Delta I_m = \frac{SEFD}{\eta_{\rm c}\sqrt{n_{\rm pol}N(N-1)t_{\rm int}\Delta\nu}}\]3

 

\[\Delta I_m = \frac{SEFD}{\eta_{\rm c}\sqrt{n_{\rm pol}N(N-1)t_{\rm int}\Delta\nu}}\]

where:

- SEFD is the "system equivalent flux density" (Jy), defined as the flux density of a radio source that doubles the system temperature. Lower values of the SEFD indicate more sensitive performance. For the EVLA's 25-meter paraboloids, the SEFD is given by the equation SEFD = 5.62Tsys/ηA, where Tsys is the total system temperature (receiver plus antenna plus sky), and ηA is the antenna aperture efficiency in the given band.
- ηc is the correlator efficiency (at least 0.92 for the EVLA).
- npol is the number of polarization products included in the image; npol = 2 for images in Stokes I, Q, U, or V, and npol = 1 for images in 'RCP' or 'LCP'.
- N is the number of antennas.
- tint is the total on-source integration time in seconds.
- Δν is the bandwidth in Hz.

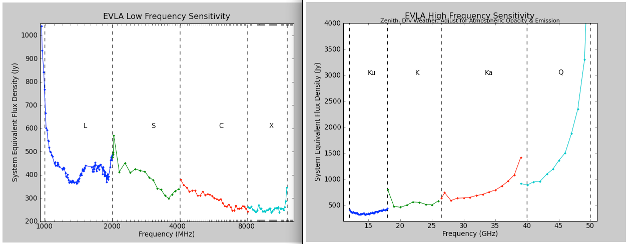
Figure 2 shows the SEFD as a function of frequency for those bands currently installed on EVLA antennas, and include the contribution to Tsys from atmospheric emission at the zenith. Table 6 gives the SEFD at some fiducial EVLA frequencies.

 

Note: SEFDs at Ku, K, Ka, and Q bands include contributions from Earth's atmosphere, and were determined under good conditions. At X-band, where the VLA-style receivers are still in use, the SEFD is approximately 310 Jy.

Note that the theoretical rms noise calculated using equation 1 is the best limit possible. There are several factors that will tend to increase the noise compared with theoretical:

  • For the more commonly-used "robust" weighting scheme, intermediate between pure natural and pure uniform weightings (available in the AIPS task IMAGR and CASA task clean), typical parameters will result in the sensitivity being a factor of about 1.2 worse than the listed values.
  • Confusion. There are two types of confusion: (i) that due to confusing sources within the synthesized beam, which affects low resolution observations the most. Table 6 shows the confusion noise in D configuration (see Condon 2002, ASP Conf. 278, 155), which should be added in quadrature to the thermal noise in estimating expected sensitivities. The confusion limits in C configuration are approximately a factor of 10 less than those in Table 6; (ii) confusion from the sidelobes of uncleaned sources lying outside the image, often from sources in the sidelobes of the primary beam. This primarily affects low frequency observations.
  • Weather. The sky and ground temperature contributions to the total system temperature increase with decreasing elevation. This effect is very strong at high frequencies, but is relatively unimportant at the other bands. The extra noise comes directly from atmospheric emission, primarily from water vapor at K-band, and from water vapor and the broad wings of the strong 60 GHz O2 transitions at Q-band.
In general, the zenith atmospheric opacity to microwave radiation is very low - typically less than 0.01 at L, C and X-bands, 0.05 to 0.2 at K-band, and 0.05 to 0.1 at the lower half of Q-band, rising to 0.3 by 49 GHz. The opacity at K-band displays strong variations with time of day and season, primarily due to the 22 GHz water vapor line. Conditions are best at night, and in the winter. Q-band opacity, dominated by atmospheric O2, is considerably less variable.
Observers should remember that clouds, especially clouds with large water droplets (read, thunderstorms!), can add appreciable noise to the system temperature. Significant increases in system temperature can, in the worst conditions, be seen at frequencies as low as 5 GHz.
Tipping scans can be used for deriving the zenith opacity during an observation. In general, tipping scans should only be needed if the calibrator used to set the flux density scale is observed at a significantly different elevation than the range of elevations over which the phase calibrator and target source are observed. When the flux density calibrator observations are within the elevation range spanned by the science observing, elevation dependent effects (including both atmospheric opacity and antenna gain dependencies) can be accounted for by fitting an elevation-dependent gain term. See the following item.
  • Antenna elevation-dependent gains. The antenna figure degrades at low elevations, leading to diminished forward gain at the shorter wavelengths. The gain-elevation effect is negligible at frequencies below 8 GHz. The antenna gains can be determined by direct measurement of the relative system gain using the AIPS task ELINT on data from a strong calibrator which has been observed over a wide range of elevation. If this is not possible, care should be taken to observe a primary flux calibrator at the same elevation as the target.

    The AIPS task INDXR applies standard elevation-dependent gains and an estimated opacity in CL table version 1. The CASA calibration tasks (e.g. gaincal, bandpass) also use the standard gain curves.

  • Pointing. The SEFD quoted above assumes good pointing. Under calm nighttime conditions, the antenna blind pointing is about 10 arcsec rms. The pointing accuracy in daytime is a little worse, due to the effects of solar heating of the antenna structures. Moderate winds have a very strong effect on both pointing and antenna figure. The maximum wind speed recommended for high frequency observing is 15 mph (7 m/s). Wind speeds near the stow limit (45 mph) will have a similar negative effect at 8 and 15 GHz.
To achieve better pointing, "referenced pointing" is recommended, where a nearby calibrator is observed in interferometer pointing mode every hour or so. The local pointing corrections thus measured can then be applied to subsequent target observations. This reduces rms pointing errors to as little as 2 - 3 arcseconds if the reference source is within about 10 degrees (in azimuth and elevation) of the target source, and the source elevation is less than 70 degrees. At source elevations greater than 80 degrees (zenith angle < 10 degrees), source tracking becomes difficult; it is recommended to avoid such source elevations during the observation preparation setup.
Use of referenced pointing is highly recommended for all K, Ka, and Q-band observations, and for lower frequency observations of objects whose total extent is a significant fraction of the antenna primary beam. It is usually recommended that the referenced pointing measurement be made at 8 GHz (X-band), regardless of what band your target observing is at, since X-band is the most sensitive, and the closest calibrator is likely to be weak. Proximity of the reference calibrator to the target source is of paramount importance; ideally the pointing sources should precede the target by 20 or 30 minutes in Right Ascension (RA). The calibrator should have at least 0.5 Jy flux density at X-band and be unresolved on all baselines to ensure an accurate solution.

To aid EVLA proposers there is an exposure tool calculator on-line at http://science.nrao.edu/facilities/evla/tools/exposure/evlaExpoCalc.jnlp that provides a graphical user interface to these equations.

The beam-averaged brightness temperature measured by a given array depends on the synthesized beam, and is related to the flux density per beam by:

\[T_{\rm b} = \frac{S \lambda^2}{2k\Omega} = F \cdot S\]

...equation (2)

where Tb is the brightness temperature (Kelvins) and Ω is the beam solid angle. For natural weighting (where the angular size of the approximately Gaussian beam is ∼ 1.5λ/Bmax), and S in mJy per beam, the constant F depends only upon array configuration and has the approximate value F = 190, 18, 1.7, 0.16 for A, B, C, and D configurations, respectively. The brightness temperature sensitivity can be obtained by substituting the rms noise, ΔIm, for S. Note that Equation 2 is a beam-averaged surface brightness; if a source size can be measured the source size and integrated flux density should be used in Equation 2, and the appropriate value of F calculated. In general the surface brightness sensitivity is also a function of the source structure and how much emission may be filtered out due to the sampling of the interferometer. A more detailed description of the relation between flux density and surface brightness is given in Chapter 7 of Reference 1, listed in Documentation.

For observers interested in HI in galaxies, a number of interest is the sensitivity of the observation to the HI mass. This is given by van Gorkom et al. (1986; AJ, 91, 791):

\[M_{\rm HI} = 2.36 \times 10^5 D^2 \sum S \Delta V ~M_\odot\]

where D is the distance to the galaxy in Mpc, and SΔV is the HI line area in units of Jy km/s.

Connect with NRAO

The National Radio Astronomy Observatory and Green Bank Observatory are facilities of the U.S. National Science Foundation operated under cooperative agreement by Associated Universities, Inc.

Founded in 1956, the NRAO provides state-of-the-art radio telescope facilities for use by the international scientific community. NRAO telescopes are open to all astronomers regardless of institutional or national affiliation. Observing time on NRAO telescopes is available on a competitive basis to qualified scientists after evaluation of research proposals on the basis of scientific merit, the capability of the instruments to do the work, and the availability of the telescope during the requested time. NRAO also provides both formal and informal programs in education and public outreach for teachers, students, the general public, and the media.

The National Science Foundation (NSF) is an independent federal agency created by Congress in 1950 "to promote the progress of science; to advance the national health, prosperity, and welfare; to secure the national defense..."

AUI collaborates with the scientific community and research sponsors to plan, build, and operate cutting-edge facilities. We cultivate excellence, deliver value, enhance education, and engage the public.