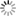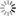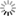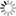Flux Density - Brightness Temperature Conversion
Start with the Rayleigh-Jeans law:
[display]T = \frac{\lambda^2}{2 \, k \, \Omega} S [/display]
where T is the brightness temperature, [inline]\lambda[/inline] the wavelength, k the Boltzmann constant, [inline]\Omega[/inline] the beam solid angle, and S the flux density, all in mks units.
Interferometric maps are measured in brightness units [inline]I[/inline] of Jy/beam, where “beam” is a nominal area over which the brightness is defined.
We replace [inline]\frac{S}{\Omega}[/inline] by [inline]\frac{S}{beam}\frac{beam}{\Omega} = I \,\frac{beam}{\Omega} [/inline], where the second term is the conversion of “beam” to a solid angle in units of steradian.
For a "dirty map", the “beam” is the "dirty beam" which has a complicated structure that depends on the number and orientation of baselines as a function of time. Once the image is deconvolved, however, the "dirty beam" is replaced by a "clean beam", a Gaussian with peak of unity and [inline]\theta_{maj}[/inline] and [inline]\theta_{min}[/inline] as the half-power beam widths along the major and minor axes, respectively.
The area of a Gaussian beam is defined by its 2-dimensional integral
[display]\Omega = \frac{\pi \, \theta_{maj} \, \theta_{min}}{4 \, \ln 2}[/display]
(see the unnumbered equation following Eq 3G4 in the NRAO Interferometers II course).
Substituting [inline]\Omega[/inline] in the first equation and converting all constants to a pre-factor leads to:
[display]T = 0.32 \times 10^{23} \frac{\lambda^2}{\theta_{maj} \, \theta_{min}}\, I[/display]
Converting to units to cm, seconds of arc, and mJy/beam results in:
[display]T = 1.36 \frac{\lambda^2}{\theta_{maj} \, \theta_{min}}\, I[/display]
or in frequencies [inline]\nu[/inline] in units of GHz:
[display]T = 1.222\times10^{3} \frac{I}{\nu^2 \, \theta_{maj} \, \theta_{min}}[/display]
