Spectral Line
The wide bandwidths of the VLA allow users to observe up to 8GHz of bandwidth at a time. All observations with the VLA are inherently spectral observations, including those intended for continuum science. The VLA's improved sensitivity and wide bandwidths greatly enhance the VLA's functionality for spectral line purposes, enabling simultaneous imaging of multiple spectral lines. The WIDAR correlator is extremely flexible and can act as up to 64 independent correlators with different bandwidths, channel numbers, polarization products, and observing frequencies. The VLA is able to:
- deliver continuous spectral coverage of up to 8GHz;
- access 1GHz or 2GHz chunks in each receiver band (called basebands) and place multiple correlator subbands within them;
- place up to 32, independently tunable subbands within a baseband, up to 64 in total. Each subband can be configured with its own subband bandwidth, number of frequency channels, and polarization products;
- fine-tune each baseband frequency independently according to an object's line-of-sight velocity with respect to the earth at the time of the observation (Doppler Setting); each subband frequency can be set to apply this shift or not.
The detailed capabilities offered for each semester are described in the VLA Observational Status Summary (OSS).
Line Frequencies and Velocity Conventions
Spectral line catalogs available online are useful for selecting targeted line rest frequencies. The recommended catalog for VLA and ALMA observing is Splatalogue which contains molecular line data from sources including the Lovas catalog, the JPL/NASA molecular database, the Cologne Database for Molecular Spectroscopy, as well as radio recombination lines.
Observing Frequency and Velocity Definitions
The sky frequency (ν) at which we must observe a spectral line is derived from the rest frequency of the spectral line (ν0), the line-of-sight velocity of the source (V), and the speed of light (c). The relativistic velocity, or true line-of-sight velocity, is related to the observed and rest frequencies by
\[V = \frac{\nu^2_0-\nu^2}{\nu^2_0+\nu^2}c\]
This equation is a bit cumbersome to use; in astronomy two different approximations are typically used:
- Optical Velocity \[V^{optical} = \frac{\lambda-\lambda_0}{\lambda_0}\,\,c = cz \] (z is the redshift of the source; λ and λ0 are the corresponding observed and rest wavelengths, respectively)
- Radio Velocity \[V^{radio} = \frac{\nu_0-\nu}{\nu_0}\,\,c = \frac{\lambda-\lambda_0}{\lambda}\,\,c \neq V^{optical} \]
The radio and optical velocities are not identical. Particularly,V optical and V radio diverge for large velocities. Optical velocities are commonly used for (Helio/Barycentric) extragalactic observations; (LSR) radio velocities are typical for Galactic observations.
At high redshifts, it is advisable to place the zero point of the velocity frame into the source by redshifting the rest frequency of the line via \[\nu=\frac{\nu_0}{z+1}\]
where the redshifted rest frequency ν can now be used as the nominal rest frequency for the observations. Zero velocity is then defined for that redshift and is therefore intrinsic to the object. This method will appropriately apply the redshift correction to the channel and line widths and the resulting velocities are also relative to the source.
Note that the VLA's natural spectral axis is in frequency. The radio convention will simply be a velocity relabeling to the frequency axis. Using the optical velocity and redshift, however, will introduce a non-linearity between channel widths and labeling, in particular for large velocity values.
Velocity Reference Frames
The Earth rotates, revolves around the Sun, rotates around the Galaxy, moves within the Local Group, and shows motion against the Cosmic Microwave Background. As for the convention above, any source velocity must therefore also always be specified relative to a reference frame.
Various velocity rest frames are used in the literature. The following table lists their name, the motion that is corrected for, and the maximum amplitude of the velocity correction. Each rest frame correction is incremental to the preceding row:
| Rest Frame Name | Rest Frame | Correct for | Max. Amplitude (km/s) |
|---|---|---|---|
| Topocentric | Telescope | Nothing | 0 |
| Geocentric | Earth Center | Earth rotation | 0.5 |
| Earth-Moon Barycentric | Earth+Moon center of mass | Motion around Earth+Moon center of mass | 0.013 |
| Heliocentric | Center of the Sun | Earth orbital motion | 30 |
| Barycentric | Earth+Sun center of mass | Earth+Sun center of mass | 0.012 |
| Local Standard of Rest (LSR) | Center of Mass of local stars | Solar motion relative to nearby stars | 20 |
| Galactocentric | Center of Milky Way | Milky Way Rotation | 230 |
| Local Group Barycentric | Local Group center of mass | Milky Way Motion | 100 |
| Virgocentric | Center of the Local Virgo supercluster | Local Group motion | 300 |
| Cosmic Microwave Background | CMB | Local Supercluster Motion | 600 |
The velocity frame should be chosen based on the science. For most observations, however, one of the following three reference frames is commonly used:
- Topocentric is the reference frame of the observatory (defining the sky frequency of the observations). Visibilities in a measurement set are typically stored in this frame.
- Local Standard of Rest is the native output of images in CASA. Note that there are two varieties of LSR: the kinematic LSR (LSRK) and the dynamic (LSRD) definitions for the kinematic and dynamic centers, respectively. In almost all cases LSRK is being used and the less precise name LSR is usually used synonymously with the more modern LSRK definition. LSR in the PST and in the OPT means LSRK.
- Barycentric is a commonly used frame that has virtually replaced the older Heliocentric standard. Given the small difference between the Barycentric and Heliocentric frames, they are frequently used interchangeably.
Doppler Correction
A telescope naturally operates at a fixed sky frequency (Topocentric velocity frame) which can be adjusted to account for the motion of the Earth. The observed frequency of a spectral line will shift during an observing campaign. Within a day, the rotation of the Earth dominates and the line may shift up to ±0.5km/s, depending on the position of the source on the sky (see the table on Velocity Rest Frames above). Observing campaigns that span a year may have spectral lines that shift by up to ±30km/s due to the Earth's motion around the Sun.
As a rule of thumb, 1 MHz in frequency corresponds roughly to x km/s for the line at a wavelength of x in mm. For example, 1 MHz corresponds to about 7 km/s in velocity at a wavelength of 7 mm, and to roughly 210 km/s at the 21 cm line. Using this rule of thumb, a line may shift by up to ±5 MHz in Q-band and by up to ±0.15 MHz in L-band over the course of a year. This shifting needs to be taken into account when setting up the dynamically scheduled observations. Accounting for the frequency shifting can be handled in different ways:
- use the same fixed sky frequency for all observations, accommodating the line shift (maximum of ±30 km/s) by using a wide enough bandwidth to cover the line at any time in the observing campaign. The data is later regridded in post processing to a common LSRK or BARY velocity frame. The actual sky frequency of a specific spectral line rest frequency can be computed with the Dopset tool for any given time. One may find the LST dates for an observation on the VLA Observing Schedules page.
- calculate the sky frequency at the beginning of an observing block and keep this fixed for the duration of the scheduling block. This is called Doppler Setting (in contrast to Doppler tracking below). The VLA supports Doppler setting. Doppler Setting can be specified for each individual baseband in the OPT, removing the burden to do this for each possible observing run by the observer. The line shift during the observation is then reduced to the rotation of the earth (maximum amplitude ±0.5 km/s). This small shift will be corrected in data processing, i.e., if the length of the observing run justifies this correction. Although the absolute sky frequency will be different between observing runs separated in time, Doppler Setting will place the spectral line in the same channel number of each repeated observation.
- change the sky frequency continuously to keep the line at the same position in the band. This method is called Doppler tracking and was standard for the VLA before the WIDAR correlator was in place. Now, the VLA does NOT support Doppler tracking. The WIDAR correlator offers enough bandwidth and spectral channels to cover any line shift and post processing regridding needs. Additionally, a non-variable sky frequency may also yield a more robust calibration and overall system stability.
The regridding of the spectrum can be completed during data processing in CASA directly during imaging in the tasks clean and tclean. Tasks cvel or mstransform provide the same functionality for the visibilities in a MeasurementSet without imaging. In AIPS, the task CVEL typically is run after bandpass calibration. Assuming one knows the spectral line width in advance, the regridding works well when the spectral features are sampled with at least 4 channels. We therefore recommend to oversample an spectral feature with at least 4 channels during the observations.
The WIDAR Correlator
The WIDAR correlator is inherently a spectral line correlator in any regular mode. A full description of the current WIDAR capabilities is provided in the WIDAR section of the OSS. The OSS also contains a spectral line configurations section.
There are two important issues when configuring the WIDAR correlator for spectral line observations. One is to set the necessary spectral resolution. This can be achieved by baseline board stacking and/or recirculation. Both are described in the OSS. For observing large instantaneous bandwidths with high spectral resolution, it is recommended to use as wide as bandwidth as possible (i.e., 128, 64 or 32 MHz) and use stacking, possibly in combination with recirculation over the alternative of using many narrow subbands stacked next to each other. This avoids the stitching process described below and provides a much better spectral baseline.
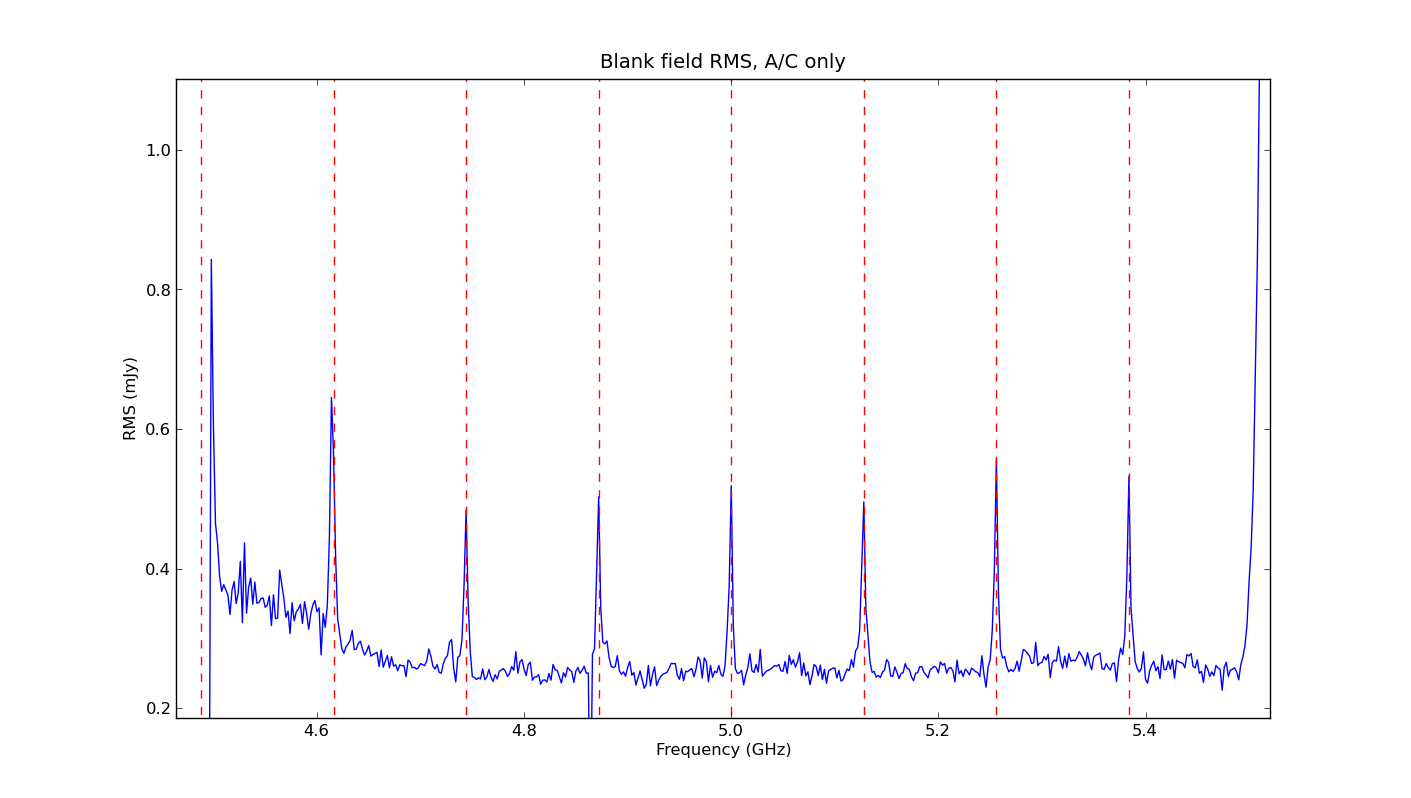
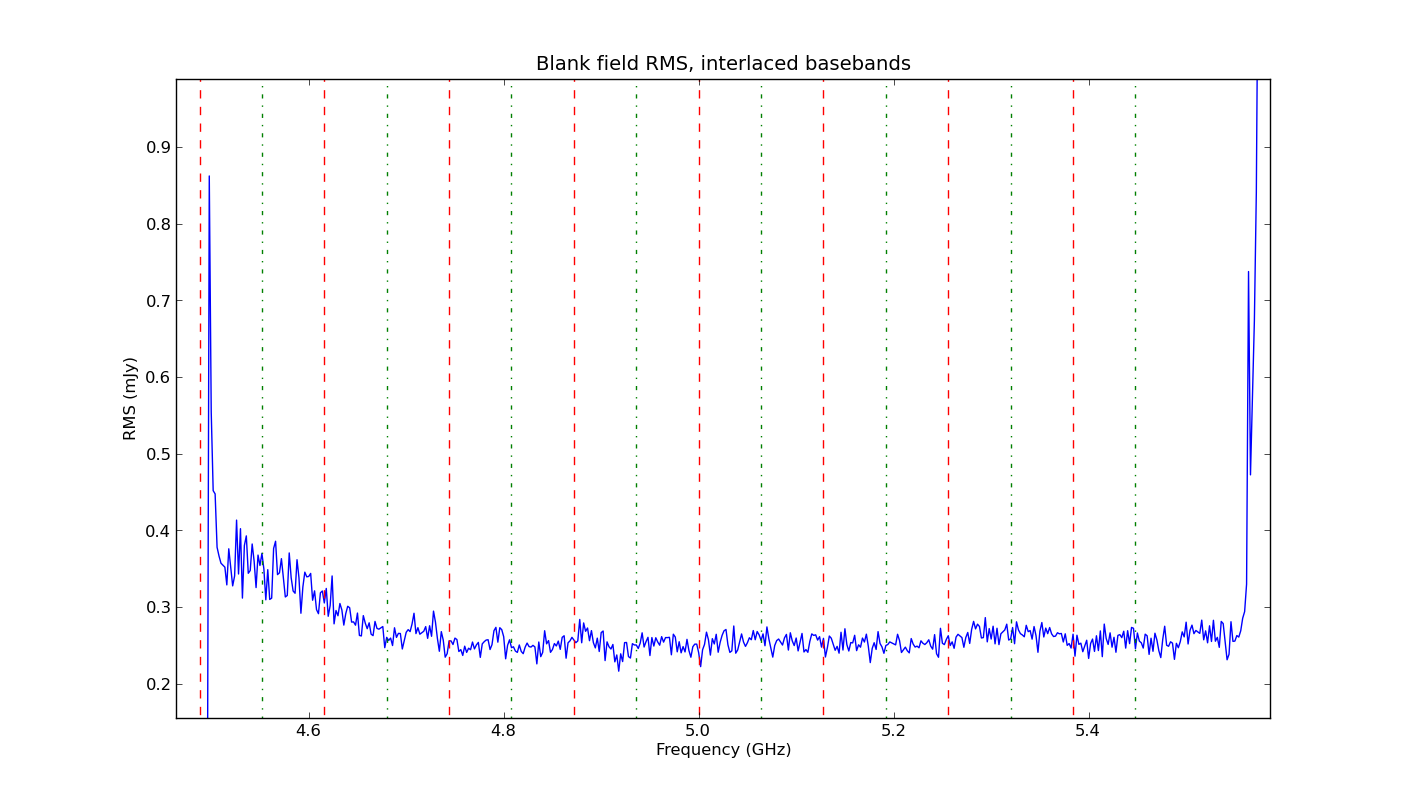
A second issue is the existence of the 128 MHz boundaries. Lines should not be placed across or very near these boundaries since subbands cannot span across a boundary and the sensitivity drops near the boundaries. In particular note that the very center of the baseband always falls on a 128 MHz boundary. The spectral line under consideration should never be placed in the very center of a baseband. Multi-line observations also need to ensure that none of the lines fall on or near a boundary. This can be challenging at times but is usually a solvable problem and the OPT provides some tools to do so. If it is not possible to obtain simultaneous coverage of all of your lines, or if the exact position of the line is unknown (e.g., for line searches), it is possible to observe with two basebands shifted by 10–64 MHz apart. This will ensure that one baseband covers the boundaries of the other baseband with full sensitivity. An example is given in the figures (8.1.1 and 8.1.2) below, where the top figure shows the RMS of a single baseband with the 128 MHz boundaries sticking out as having high noise. The bottom figure shows a combination of two basebands that have been separated by 64MHz. The noise spikes are clearly suppressed by adding, with the appropriate weight, the two basebands, or even by simply replacing the noisy channels of each baseband with data from the other.
Subband 0
The baseband response is suppressed at each side of the spectrum. The largest affected baseband edge is at the highest sky frequency in the baseband when using lower sideband in X and Ku-bands, and at the lowest sky frequency in the baseband when using upper sideband in observing bands other than X and Ku-bands. For upper sideband, this causes reduced sensitivity typically in the lower 20% frequency edge of the first 128 MHz subband and about 5% in the higher frequency edge of the last 128 MHz subband of a baseband (the reverse is happening for X and Ku-bands). It is typically noticed in subband 0 of a baseband, but other subband numbers are possible as well. This part of the spectrum, the lower ~30 MHz and upper ~8 MHz of each baseband in 4, P, L, S, C, K, Ka, and Q-bands or the lower ~8 MHz and upper ~30 MHz of each baseband in X and Ku-bands, should be avoided for spectral line observing if possible. This effect can readily be seen in the figures 7.1.1 and 7.1.2 above, where the RMS in the subband below 4.6 GHz is significantly increased. See EVLA memo 154 for details.
Data Rate Limits
A high number of subbands, baseline board stacking, recirculation, and time resolution can add up to an extremely high data rate in the correlator. Please see the OSS for the allowable data rates and volumes for each observing semester. The OPT instrument configuration calculates data rates based on the spectral line setup and the sum of data rates and total volume must not exceed the maximum allowed for any observational setup.
Preparing Spectral Line Observations
The Observation Preparation Tool (OPT) is the web-based interface to create scheduling blocks (SBs) for time awarded on the VLA. An SB is the observing schedule used for a single observing run. This consists of at least a start-up scan sequence (see the 8/3-Bit Attenuation and Setup Scans guidelines), a bandpass calibrator, a flux density calibrator, a complex gain calibrator, and target observations. High frequency observations should also include at least two (often more) X band interferometric pointing scans and a corresponding setup scan, whereas 3-bit and multi-frequency band observations add even more required scans to the SB. In the OPT, the observer specifies the sources, scan lengths and order, and correlator setups. A full project may consist of several SBs. To access the OPT, go to my.nrao.edu and click on the Obs Prep tab, followed by Login to the Observation Preparation Tool. Instructions for using the OPT and for selecting appropriate calibrators are provided in the OPT Manual.
Bandpass Setup
All observations with the VLA—even those with the goal of observing continuum—require bandpass calibration. When scheduling the bandpass calibration scans within an SB, the observer should be careful to minimize the number of shadowed antennas, as an antenna without a bandpass determined for it will essentially be flagged in the data for the rest of the observation. A bandpass calibrator should be bright enough, or observed long enough, so that the bandpass calibration does not significantly contribute to the noise in the image. For a given channel width a bandpass calibrator with flux density Scal observed for a time tcal and a science target with flux density Sobj observed for a time tobj, 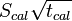 should be greater than
should be greater than 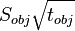 . How many times greater will be determined by one's science goals and the practicalities of the observations, but
. How many times greater will be determined by one's science goals and the practicalities of the observations, but 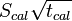 should be greater by at least a factor of two. For extremely narrow channels or very weak bandpass calibrators, those typical flux requirements can lead to extremely large integration times. As an alternative one may then choose to reduce the integration time and interpolate in frequency, or to fit a polynomial across all channels in post-processing (bandtype=BPOLY in CASA's bandpass task).
should be greater by at least a factor of two. For extremely narrow channels or very weak bandpass calibrators, those typical flux requirements can lead to extremely large integration times. As an alternative one may then choose to reduce the integration time and interpolate in frequency, or to fit a polynomial across all channels in post-processing (bandtype=BPOLY in CASA's bandpass task).
The bandpass calibrator should be a point source or have a well-known model. At low frequencies, the absolute flux density calibrators (3C48, 3C147, or 3C286) are quite strong and can often double as bandpass calibrators. At high frequencies (Ku, K, Ka, and Q-bands), however, these sources have only moderate flux densities of ~0.5–3 Jy, translating into a potentially noisy bandpass solution. A different, stronger bandpass calibrator should then be observed. Naturally, all of the above depends on the channel widths, and for wide channels the standard flux calibrators may be sufficient even at higher frequencies. In turn, extremely narrow channels may require stronger bandpass calibrators at the low frequency end. Additionally, we have shown that one can transfer the bandpass from a wide subband onto a narrow subband if the wide bandpass frequency range covers the narrow one. This may be good to a level of a few percent, but we advise to use that option only when absolutely necessary.
The stability of bandpasses as a function of time is of concern for high-dynamic-range spectral work as well as for weak broad lines. We have found that most antennas show bandpasses that are stable to a few (~2–4) parts in a thousand over a period of several (~4–8) hours. This should be sufficient for most scientific goals but the bandpasses can be observed several times during an observation for extreme calibration accuracy requirements.
A complication can occur when the frequency range of the bandpass is contaminated by other spectral features, such as RFI lines or Galactic HI in absorption or emission. There are two basic options to accommodate that situation:
- if the feature is narrow, one can simply observe as usual. In post processing, the narrow feature can be flagged and the frequency gap interpolated by values of nearby channels or by fitting a polynomial across the bandpass.
- for wider contaminating lines, an option is to observe the bandpass at slightly offset frequencies and transfer the bandpass to the target frequency. If a common solution is obtained from two, symmetric offsets, at higher and lower frequencies, the solution can be improved. Depending on the choice of offsets, and also on the position in the receiver frequency range, the error can vary. For 4 MHz offsets close to the HI rest frequency of 1.42 GHz, the error is in the percent range.
Complex Gain Calibration
The complex gain (phase and amplitude gain) calibration is the same for a spectral line observation as for any other observation. Ideally, one should use the same correlator setup for the complex gain calibrator and the science target. For weak calibrators, however, it is possible to use wider bandwidths for the phase calibrator and then transfer the phases to the source. However, there will be a phase offset between them. The phase offset between the narrow and wide subbands can be determined by observing a strong source at both setups (e.g. the bandpass calibrator) and applied in post processing from the complex gain calibrator to the target sources. A similar method can be used if the complex gain calibrator is observed at a slightly different frequency, e.g. to avoid a contaminating line feature such as Galactic HI.




Connect with NRAO